i小学奥数可加存眷
上 网课、下 材料 、数学进修好辅佐
人教版小学五年级数学上册
易错题复习( 1)
01填空题。
1、1.25×0.8表达 。
2、往掉0.25的小数点,就是把那个数扩展;把50.4的小数点向左挪动两位,就是把它缩小到本来的 。
3、两个因数相乘,一个因数扩展10倍,另一个因数扩展3倍,积会。
4.一个不为0的数乘以0.8,它的积比那个数。一个天然数乘以0.01,就是把那个天然数。
5、把“2.58×0.03”中的0.03扩展为3而使积稳定,另一个因数2.58的小数点应,积保留两位小数是。
6、56÷11的商用轮回小数表达是切确到百分位是。
7、3÷11的商用轮回小数的简便写法记做商保留一位小数是。
8、9.97÷4.21的商保留两位小数是保留整数是。
9、在“ ”中,最小的是,更大的是。
10、两个因数的积是3.4,假设把两个因数同时扩展10倍,积是
11、三个2.5连乘得积是。
12、3x=6.9的解是。
13、生果店运来香蕉x千克,运来的桃子是香蕉的2.5倍,香蕉和桃子一共运来 千克。假设x=5,桃子比香蕉多千克。
14、35 dm 2 = cm 2 ;7.4 m 2 =d m 2 ;7.5 m 2 =cm;2350 m 2 =公顷;500平方米=公顷;3平方米70平方分米=平方米;3小时15分=小时;1.8时=时分;2.15小时=分钟;7.6米=米厘米。
15、把一个平行四边形木框拉成一个长方形,周长,它的高和面积城市
16、把一个长方 形木框拉成一个平行四边形,周长,它的高和面积城市。
17、把一个平行四边形沿高剪开,从头拼成一个长方形,它的高和面积,周长。
展开全文
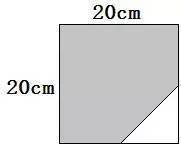
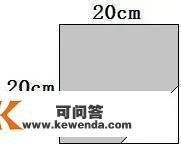
18、一张边长是20厘米的正方形纸,从相邻两边的中点连一条线段(如下图),沿那条线段剪往一个角,剩下的(暗影部门)面积是 cm2 。
19、一个三角形和一个平行四边形底相等面积也相等。平行四边形的高是10cm,三角形的高是 。
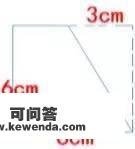
20、一个梯形的上底增加3厘米后就酿成一个边长6厘米的正方形(如下图),那个梯形的面积是平方厘米。
21、把一个小数的小数点向右挪动两位,得到一个新数,与原数相差44.55,原数是。
22、一个曲角三角形的三条边别离是3cm、4cm和5cm,那个三角形的面积是,斜边上的高是。
23、一个小数有两位小数,保留一位小数它的近似值是10.0,那个数更大是最小。
24、三个持续天然数,中间的数是n,别的的两个数别离是和。
25、125缩小到它的是0.125;扩展到它的100倍是0.3。
26、一个两位数,它的个位上的数字是b,十位上的数字是a,那么那个两位数可写成。
27、一个等腰三角形的底是16cm,腰是a cm,高是b cm。那个三角形的周长是cm,面积是 cm2 。
28、一个等腰三角形的周长是16厘米,腰长是5厘米,底边上的高是4厘米,它的面积是平方厘米。
29、把一个边长8厘米的正方形剪拼成一个平行四边形后面积是。
30、0.25除以0.15,当商是1.6时,余数是;0.79÷0.04,商是19,余数是。
31、一个梯形的上底、下底、高别离是5cm、9cm、6cm,面积是平方分米。
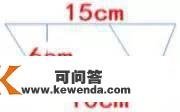
32、 小明从一个上底是15cm、下底是10cm、高是6cm的梯形中剪下一个平行四边形(如下图)。那个平行四边形的面积是cm2 。
33、一堆圆木,最顶层有5根,更底层有14根。每相邻两层相差1根圆木,那堆圆木一共有根。
34、一个三角形和一个平行四边形的面积相等,高也相等。假设三角形的底是25cm,平行四边形的底是dm。
35、一个曲角梯形,假设把下底削减3cm,那个梯形就酿成一个边长7cm的正方形。那个梯形的面积是 cm2 。
36、张诚把一个梯形的上底缩小成一点后 那个梯形就酿成一个形。
02揣度题。
1、小数乘法的意义和整数乘法的意义完全不异。
2、一个数乘0.8,积比本来的数小。
3、近似数7.0和7的大小相等,但切确度纷歧样。
4、8.4×0.5就是求8.4的一半是几。
5、一个数除以一个小数,商可能是小数。
6、小数除以小数,商必然是小数。
7、在除法里:商必然小于被除数。
8、一个非0的数除以一个比1小的小数,所得的商必然比被除数大。
9、假设除数小于1,那么商就比被除数(0除外)大。
10、(0.1-0.1×0.1)÷0.1=0.9。
11、 x2 不成能等于2x。
12、 a2 >2a。
13、未知数的值喊做方程的解。
14、小数分有限小数、无限小数和轮回小数。
15、一组数据的中位数和均匀数可能相等。
16、轮回小数纷歧定是无限小数。
17、方程摆布两边同时乘一个不异的数,摆布两边仍然相等。
18、把平行四边形木框拉生长方形,周长和面积都变大了。
19、假设两个图形能拼成平行四边形,那么它们必然完全一样。
20、边长是4分米的正方形,它的周长和面积相等。
21、两个都比1小的数(0除外)相乘,积必然小于此中的每一个因数。
22、方程5+2x=16.2的解是5.6。
23、6x+6=6(x+1)。
24、把一个梯形的上底、下底和高都扩展2倍,它的面积就扩展2倍。
03抉择题。
1、a与它的2.5倍相差。
A、a-2.5 B、2.5-a C、1.5a
2、下面两个式子相等的是。
A、a+a和2a B、a×2和 a2 C、a+a和 a2
3、与3.75÷12.5成果不异的算式是。
A、3750÷12.5 B、37.5÷125 C、3750÷125
4、能够运用对4.7×99+4.7停止简便运算。
A、乘法交换律 B、乘法连系律 C、乘法分配律
5、已知两个因数的积是此中一个因数的3.5倍,是另一个因数的4.2倍,那两个因数的积是。
A、8.7 B、14.7 C、1.2
6、下面算式中积最小的是。
A、320×0.24 B、2.4×0.32 C、24×0.32
04列方程或算式。
1、“3.2除x的商是0.8”的等量关系式是__________________
2、一个数的3倍加上那个数的一半等于80.5,求那个数。
(列方程)解:设那个数是x,则方程是:__________________
3、一个数的5倍与它的3.6倍相差5.6,求那个数。
(列方程)解:设那个数是x,则方程是:__________________
4、“7与0.38的和往除4.6,商是几?”的算式是__________________
05利用题。
1、某小学五年级有学生55小我。男生人数是女生人数的1.2倍。男、女生各有几人?
2、童拆厂本来做一种儿童服拆,每套用布2.2米。如今改进了裁剪办法,每套节约布0.2米。本来做1800套如许的服拆所用的布,如今能够多做几套?
3、一个长方形的周长是45厘米,长是宽的2倍。那个长方形的面积是几平方厘米?
4、甲乙两筐苹果,甲筐苹果的个数是乙筐的2.4倍,假设从甲筐取出35个苹果放进乙筐,那时两筐苹果个数相等,本来两筐苹果各有几个?(列方程解答)
5、妈妈将一些奶糖和生果糖分拆在小袋里,每袋拆进0.25千克奶糖和0.15千克生果糖。当生果糖用往4.5千克时,用往奶糖几千克?
6、姐姐骑电瓶车每小时行18千米,弟弟开小汽车每小时行54千米。他俩从相距247千米的两地同时相向而行,2.5小时后两人还相距几千米?
易错题复习(1)参考谜底
01填空题。
1、1.25×0.8表达 ( 1.25与0.8的积是几)。
2、往掉0.25的小数点,就是把那个数扩展( 100倍);把50.4的小数点向左挪动两位,就是把它缩小到本来的 ( 百分之一)。
3、两个因数相乘,一个因数扩展10倍,另一个因数扩展3倍,积会( 30倍)。
4.一个不为0的数乘以0.8,它的积比那个数( 小)。一个天然数乘以0.01,就是把那个天然数( 缩小到那个天然数的百分之一 或缩小100倍)。
5、把“2.58×0.03”中的0.03扩展为3而使积稳定,另一个因数2.58的小数点应 ( 向左挪动两位) ,积保留两位小数是( 0.08)。
6、56÷11的商用轮回小数表达是( 5.090909……),切确到百分位是( 5.09)。
7、3÷11的商用轮回小数的简便写法记做( ),商保留一位小数是( 0.3)。
8、9.97÷4.21的商保留两位小数是 ( 2.37) 保留整数是( 2)。
9、在“ ”中,最小的是( ),更大的是( 3.23)。
10、两个因数的积是3.4,假设把两个因数同时扩展10倍,积是( 340)
11、三个2.5连乘得积是( 15.625)。
12、3x=6.9的解是( 2.3)。
13、生果店运来香蕉x千克,运来的桃子是香蕉的2.5倍,香蕉和桃子一共运来( 3.5x) 千克。假设x=5,桃子比香蕉多( 7.5)千克。
14、35 dm 2 =( 3500) cm 2 ;7.4 m 2 =( 740)d m 2 ;
7.5 m2 =( 75000) cm 2 ;2350 m 2 =( 0.235)公顷;
500平方米=( 0.05)公顷;3平方米70平方分米=( 3.7)平方米;
3小时15分=( 3.25)小时;1.8时=( 1)时( 48)分;
2.15小时=( 129)分钟;7.6米=( 7)米( 60)厘米。
15、把一个平行四边形木框拉成一个长方形,周长( 稳定),它的高和面积城市( 变大)
16、把一个长方 形木框拉成一个平行四边形,周长( 稳定),它的高和面积城市( 变小)。
17、把一个平行四边形沿高剪开,从头拼成一个长方形,它的高和面积( 稳定),周长( 变小)。
18、一张边长是20厘米的正方形纸,从相邻两边的中点连一条线段(如下图),沿那条线段剪往一个角,剩下的(暗影部门)面积是( 350) cm2 。
19、一个三角形和一个平行四边形底相等、面积也相等。平行四边形的高是10cm,三角形的高是 ( 20cm) 。
【解析:一个三角形和一个平行四边形在底相等,面积也相等的情状下,三角形的高是平行四边形的两倍。】
20、一个梯形的上底增加3厘米后就酿成一个边长6厘米的正方形(如下图),那个梯形的面积是( 27)平方厘米。
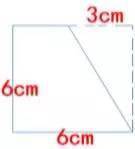
21、把一个小数的小数点向右挪动两位,得到一个新数,与原数相差44.55,原数是(0.45)。 【解析:把一个小数的小数点向右挪动两位,本来小数扩展100倍,也就是增加99倍,所以原数是:44.55÷99=0.45】
22、一个曲角三角形的三条边别离是3cm、4cm和5cm,那个三角形的面积是( 6cm2 ),斜边上的高是( 2.4cm)。 【解析:曲角三角形的三条边中,斜边是最长的,所以两条曲角边别离3cm、4cm。两条曲角边相当于那个曲角三角形的底和高所以,三角形的面积=3×4 ÷2=6 cm2 ,则斜边上的高=6 ×2 ÷5=2.4cm】
23、一个小数有两位小数,保留一位小数它的近似值是10.0,那个数更大是( 10.04)最小( 9.95)。
24、三个持续天然数,中间的数是n,别的的两个数别离是( n-1)和( n+1)。
25、125缩小到它的( 千分之一)是0.125;( 0.003)扩展到它的100倍是0.3。
26、一个两位数,它的个位上的数字是b,十位上的数字是a,那么那个两位数可写成( ab)。
27、一个等腰三角形的底是16cm,腰是a cm,高是b cm。那个三角形的周长是( 2a+16)cm,面积是( 8b) cm2 。
28、一个等腰三角形的周长是16厘米,腰长是5厘米,底边上的高是4厘米,它的面积是( 12)平方厘米。 【解析:起首要求出,底=16-5×2=6cm,然后计算,面积=6 ×4 ÷2=12 cm2 】
29、把一个边长8厘米的正方形剪拼成一个平行四边形后面积是( 64平方厘米)。 【解析:用剪拼的办法改动了外形,面积是不会变的。只要用拉抻的办法改动外形,面积才会变。】
30、0.25除以0.15,当商是1.6时,余数是( 10);0.79÷0.04,商是19,余数是( 3)。
31、一个梯形的上底、下底、高别离是5cm、9cm、6cm,面积是( 0.42)平方分米。 【解析:重视面积单元的转化。】
32、 小明从一个上底是15cm、下底是10cm、高是6cm的梯形中剪下一个平行四边形(如下图)。那个平行四边形的面积是( 60) cm2 。
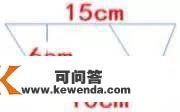
33、一堆圆木,最顶层有5根,更底层有14根。每相邻两层相差1根圆木,那堆圆木一共有( 95)根。 【解析:本题关键是要算出那堆圆木的层数:14-5+1=10层,就能够计算圆木的根数:(5+14) ×10 ÷2=95根】
34、一个三角形和一个平行四边形的面积相等,高也相等。假设三角形的底是25cm,平行四边形的底是( 1.25)dm。 【解析:重视长度单元。 一个三角形和一个平行四边形在面积相等,高也相等的情状下,平行四边形的底只是三角形的一半。】
35、一个曲角梯形,假设把下底削减3cm,那个梯形就酿成一个边长7cm的正方形。那个梯形的面积是( 59.5) cm2 。
36、张诚把一个梯形的上底缩小成一点后 那个梯形就酿成一个( 三角)形。
02揣度题。
1、小数乘法的意义和整数乘法的意义完全不异。(×)
【解析:
小数乘整数的意义与整数乘法的意义不异;而小数乘小数的意义与整数乘法的意义就不不异了;
填补:
整数乘法的意义:求几个不异加数的和的简便运算;
现有教材的理解已较宽:如3×4既能够说:3个4是几?也能够表述成:4个3是几?
小数乘法的意义:(原有老教材是分隔的,供参考)
(1)小数乘整数:与整数乘法的意义不异,就是求几个不异加数的和的简便运算.例如:2.5×6 表达6个2.5乞降或2.5的6倍是几.
(2)一个数乘小数的意义:与整数乘法的意义有所差别,它是整数乘法意义的进一步扩展.它能够理解为是求那个数的非常之几、百分几、千分之几……是几.例如,2.5 × 0.6表达2.5的非常之六是几,2.5 × 0.98表达2.5的百分之九十八是几.
记得现行教材同一为:就是求一个数的几倍(几分之几)是几?
分数乘法的意义理解与小数乘法不异。】
2、一个数乘0.8,积比本来的数小。( ×)
【解析:那个数只要大于0的时候, 乘0.8,积才比本来的数小。】
3、近似数7.0和7的大小相等,但切确度纷歧样。( √)
【解析:对。根据四舍五进的规则,7.0在数值上等于7,但是在切确位上7.0的切确位是在最初一位,在非常位,7的切确位在个位,所以他们的切确位其实不一样,即原题是对的。】
4、8.4×0.5就是求8.4的一半是几。( √)
5、一个数除以一个小数,商可能是小数。( √)
6、小数除以小数,商必然是小数。( ×)
7、在除法里:商必然小于被除数。( ×)
8、一个非0的数除以一个比1小的小数,所得的商必然比被除数大。( √)
【解析:那道题假设局限在本册常识内,它就是对的;假设那个比1小的小数是个负数,那么所得的商就会比被除数小,如:2÷(-0.5)=-4,那时候原题就是错的。那道题出在小学阶段里,自己就没有意义。】
9、假设除数小于1,那么商就比被除数(0除外)大。( √) 【解析:与上题同解。】
10、(0.1-0.1×0.1)÷0.1=0.9。( √)
11、 x2 不成能等于2x。( ×)
【解析:假设x=2,那么 x2 就会等于2x】
12、 a2 >2a。( ×)
【解析:只要a大于2时才是对的。 假设a≤2,那么a2 ≤2a 】
13、未知数的值喊做方程的解。( ×)
【解析:错。准确的说法是:使方程摆布两边相等的未知数的值喊做方程的解】
14、小数分有限小数、无限小数和轮回小数。( ×)
【解析:错。 轮回小数已经包罗在无限小数中。小数分有限小数和无限小数两大类,而无限小数再分为无限轮回小数和无限不轮回小数。】
15、一组数据的中位数和均匀数可能相等。( √)
【解析:准确。如1,2,3那组数里,2是中位数,也是均匀数,是相等的。】
16、轮回小数纷歧定是无限小数。( ×)
【 解析:错。 轮回小数自己就是无限小数。】
17、方程摆布两边同时乘一个不异的数,摆布两边仍然相等。( ×)
【解析:等式的性量是:方程两边同时乘或除以统一个数(0除外),等式仍然成立,题干中没说0除外,所以原题说法错误。】
18、把平行四边形木框拉生长方形,周长和面积都变大了。( ×)
【解析:错。 把平行四边形木框拉生长方形,四条边的长度是不会变的,所以周长不会变,只要面积变大了。】
19、假设两个图形能拼成平行四边形,那么它们必然完全一样。( ×)
【解析:错。把一个平行四边形剪成一大一小的两个平行四边形来理解就大白了。】
20、边长是4分米的正方形,它的周长和面积相等。( ×)
【解析:错。它们的数值固然不异,但单元意义纷歧样,所以是不成能说周长和面积相等。】
21、两个都比1小的数(0除外)相乘,积必然小于此中的每一个因数。( √)
22、方程5+2x=16.2的解是5.6。( √)
23、6x+6=6(x+1)。( √)
【解析:对。根据乘法分配律,那个等式是成立的。】
24、把一个梯形的上底、下底和高都扩展2倍,它的面积就扩展2倍。( ×)
【解析:错。假设本来的上底、下底、高别离是2cm、3cm、4cm,则面积是10平方厘米; 上底、下底、高都扩展2倍后, 上底、下底、高别离是4cm、6cm、8cm,面积是40平方厘米,面积不行扩展2倍,而是4倍了。】
03抉择题。
1、a与它的2.5倍相差( C)。
A、a-2.5 B、2.5-a C、1.5a
【解析:2.5a-a=1.5a】
2、下面两个式子相等的是( A)。
A、a+a和2a B、a×2和 a2 C、a+a和 a2
【解析: a+a和2a都表达两个a的和,所以那两个式子相等。】
3、与3.75÷12.5成果不异的算式是( B)。
A、3750÷12.5 B、37.5÷125 C、3750÷125
【解析:被除数与除数同时扩展10倍,商的大小稳定。 】
4、能够运用( C)对4.7×99+4.7停止简便运算。
A、乘法交换律 B、乘法连系律 C、乘法分配律
5、已知两个因数的积是此中一个因数的3.5倍,是另一个因数的4.2倍,那两个因数的积是( B)。
A、8.7 B、14.7 C、1.2
【解析:两个因数的积是此中一个因数的3.5倍(即另一个因数为3.5),是另一个因数的4.2倍(即那一个因数为4.2)则那两个因数的积是:3.5×4.2=14.7】
6、下面算式中积最小的是( B)。
A、320×0.24 B、2.4×0.32 C、24×0.32
【解析:不消计算,就用揣度积的小数位数的办法来抉择。】
04列方程或算式。
1、“3.2除x的商是0.8”的等量关系式是x÷3.2=0.8
【解析:重视“除”跟“除以”是差别的。 “除”表达它前面的数是除数, “除以”表达它前面的数是被除数。】
2、一个数的3倍加上那个数的一半等于80.5,求那个数。
(列方程)解:设那个数是x,则方程是: 3x+x ÷2=80.5
3、一个数的5倍与它的3.6倍相差5.6,求那个数。
(列方程)解:设那个数是x,则方程是: 5x-3.6x=5.6
4、“7与0.38的和往除4.6。商是几?”的算式是 4.6 ÷(7+0.38)
05利用题。
1、某小学五年级有学生55小我。男生人数是女生人数的1.2倍。男、女生各有几人
【解析:根据等量关系式 男生人数+女生人数=全班人数 列方程。】
解:设女生有x人,则男生有1.2x人
1.2x+x=55
2.2x=55
x=55 ÷2.2
x=25
男生人数=1.2x=1.2×2.5=30(人)
答:(略)
2、童拆厂本来做一种儿童服拆,每套用布2.2米。如今改进了裁剪办法,每套节约布0.2米。本来做1800套如许的服拆所用的布,如今能够多做几套?
【解析:要求如今能够多做几套,需晓得本来做的套数(已知)与如今做的套数,要求如今做的套数,还需先求出布的总米数( 1800×2.2)和如今每套用布的米数 (2.2-0.2),然后算呈现在能够做的套数 1800×2.2÷(2.2-0.2)。由此找出前提列出算式处理问题】
1800×2.2÷(2.2-0.2)-1800=180(套)
答:(略)
3、一个长方形的周长是45厘米,长是宽的2倍。那个长方形的面积是几平方厘米?
【解析:根据周长和已知 长是宽的2倍那两个信息能够操纵方程算出长和宽各是几(根据“ (长+宽) ×2=长方形周长”那个长方形周长公式列出方程),然后就能够计算长方形的面积 。 】
解:设宽是x厘米,则长是2x厘米。
(2x+x) ×2=45
3x=45÷2
3x=22.5
x=22.5÷3
x=7.5
则长=2x=2 ×7.5=15厘米
长方形的面积:15×7.5=112.5(平方厘米)
答:(略)
4、甲乙两筐苹果,甲筐苹果的个数是乙筐的2.4倍,假设从甲筐取出35个苹果放进乙筐,那时两筐苹果个数相等,本来两筐苹果各有几个?(列方程解答)
解:设乙筐的苹果有x个,则甲筐的苹果有2.4x个。
2.4x-35=x+35
2.4x-x=35+35
1.4x=70
x=70 ÷1.4
x=50
则甲筐的苹果有:2.4x=2.4×50=120(个)
答:甲筐苹果有120个,乙筐苹果有50个。
5、妈妈将一些奶糖和生果糖分拆在小袋里,每袋拆进0.25千克奶糖和0.15千克生果糖。当生果糖用往4.5千克时,用往奶糖几千克?
【解析:根据生果糖用往的量量算出用往了几袋,再乘每袋包罗奶糖的量量就能够了。】
4.5 ÷0.15 ×0.25
=30×0.25
=7.5(千克)
答:(略)
6、姐姐骑电瓶车每小时行18千米,弟弟开小汽车每小时行54千米。他俩从相距247千米的两地同时相向而行,2.5小时后两人还相距几千米?
247-(18+54) ×2.5
=247-72 ×2.5
=247-180
=67(千米) 答:(略)
存眷i小 学 奥 数微信公号
