粘滞流体流速若何随时间演化？《张向阳的物理课》求解圆柱形管中含时NS方程

在恒定压差下圆柱形管中粘滞流体的流速场若何随时间演化？怎么求解圆柱形管中的含时NS方程？若何用幂级数解法求解贝塞尔方程？《张向阳的物理课》第一百一十五期在1月14日12时开播，搜狐开创人、董事局主席兼CEO张向阳坐镇搜狐视频曲播间，先给网友们复习了差别情状下的纳维尔-斯托克斯方程的特征，随后研究恒定截面的圆管中的流体，在恒定压差下从静行起头到流速不变下来，流速场的演化过程。他先根据无限长时间的渐停止为化简纳维尔-斯托克斯方程，操纵别离变量法将方程的时间与空间别离，此中空间部门的微分方程化为贝塞尔方程。之后摘用微分方程的幂级数解法求解贝塞尔方程，推导出递推公式并得到0阶贝塞尔函数，进一步根据鸿沟前提确定了流速散布的形式，并引出了傅里叶-贝塞尔级数。

阐发含时NS方程的渐停止为 别离变量得到贝塞尔方程

在之前的曲播课程中，张向阳介绍了流体力学中的根本概念，并推导了纳维尔-斯托克斯方程：

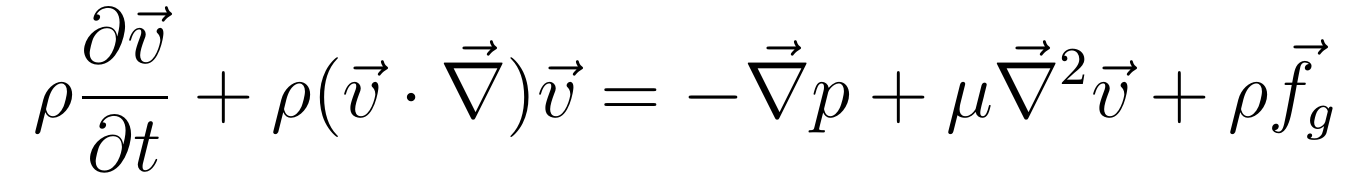
纳维尔-斯托克斯方程反映了不成压缩粘性流体活动的根本力学法例，它是一个非线性偏微分方程，一般情状下很难求解。之前的课程只讨论稳恒活动的情状，上述方程中关于时间偏导的项为零；即使如斯，当流管外形不规则的时候，上式中的第二项不为零，此时若粘滞系数项也不为零，方程仍然很复杂。那里的外形规则是指流管的横截面外形大小方位处处不异，即截面恒定的情状，不称心此前提则称为外形不规则。

展开全文

所以在之前的课程中，关于外形不规则流管，张向阳要求粘滞系数为零，如许根据纳维尔-斯托克斯方程能够推导出伯努利原理。关于外形规则流管，流体微元的运动能够不具有加速度，流体能够做泊肃叶活动，所以上式的第二项为零，如许能够考虑粘滞系数不为零的情状，那时压强梯度与流体之间的粘滞力相抗衡，构成稳恒层流。但之前讨论的都是流速场与时间无关的稳恒活动，那节课将进军含时速度场的情状，详细是研究恒定截面的圆管中的流体，在恒定压差下从静行起头到流速不变下来，流速场的演化过程。

与推导泊肃叶定律的情形类似，流体在一个半径为R的圆柱形管中活动，以管中心轴为z轴，成立柱坐标系。假设流体只要沿着z标的目的的速度，且具有绕z轴的扭转对称性。那么因为流体不成压缩，由流量守恒可知速度与坐标z无关，柱坐标系中流体的速度场能够写成：

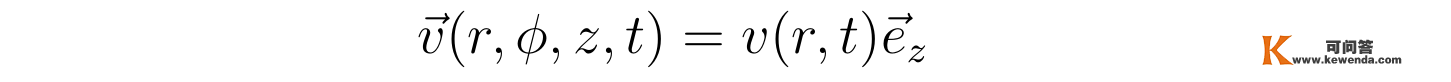
此中，e_z是沿z轴正标的目的的单元向量。

因为流速与z无关，可得上述纳维尔-斯托克斯方程的第二项为零：

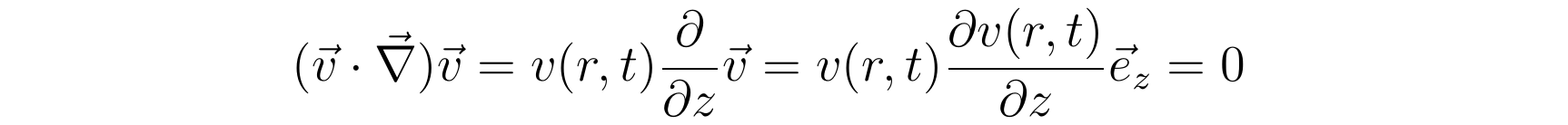
在不考虑重力场的情状下，纳维尔-斯托克斯方程能够简写成：

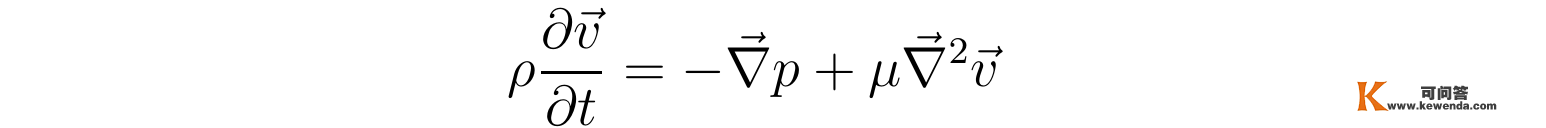
跟之前稳恒层流的阐发类似，那里流速只要z重量，所以压强梯度也只要z重量，即压强沿着径向与角向都不会改变，别的因为流速与z无关，根据上述方程可知压强梯度与z无关，连系压强沿着径向与角向都不改变的性量，随便推得压强梯度的z重量是关于全空间的一个常数-c(t),为了便利后续求解，那里要求该常数与时间t无关，于是压强梯度可写为：

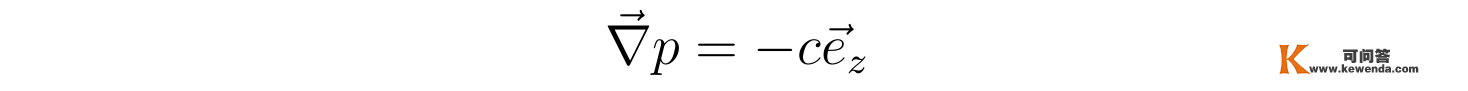
因为流速沿z轴正标的目的，上式加了负号使得c0，详细为：

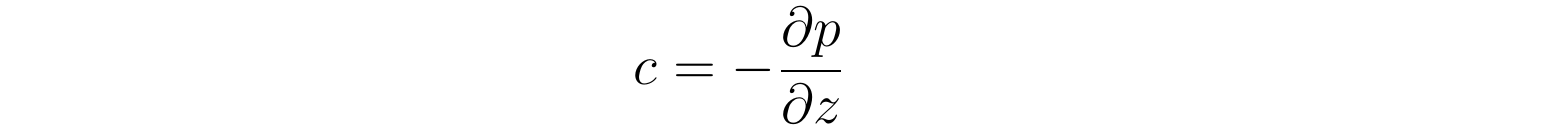
那么恒定压强的纳维尔-斯托克斯方程的z重量为：

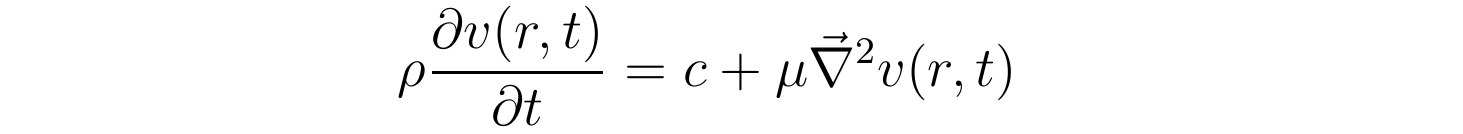
为了求解上述方程，张向阳接下来阐发含时流速散布在时间趋于无限时的渐停止为。刚起头管内全空间的流速都为零，在恒定压强的驱动下起头加速活动；但跟着流速的增加，障碍流体运动的粘滞力也随之增加，曲至与恒定压强梯度形成的驱动力相平衡。所以，跟着时间的流逝，流速不会增大到无限，而是趋于一个不变值，即在时间趋于无限时有：

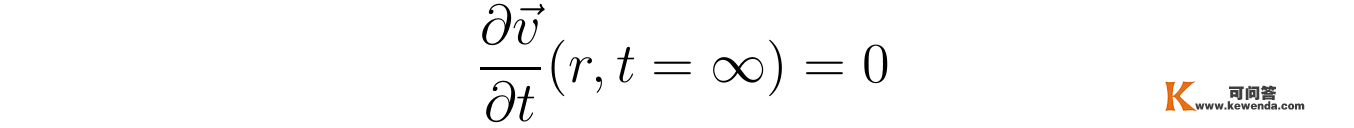
于是，在时间趋于无限时，上述关于流速散布的含时方程，酿成稳恒活动的不含时方程，在推导泊肃叶定律时已经解过该方程并得到抛物线型的流速散布，设函数f(r)为该稳恒形态的抛物线型流速散布：

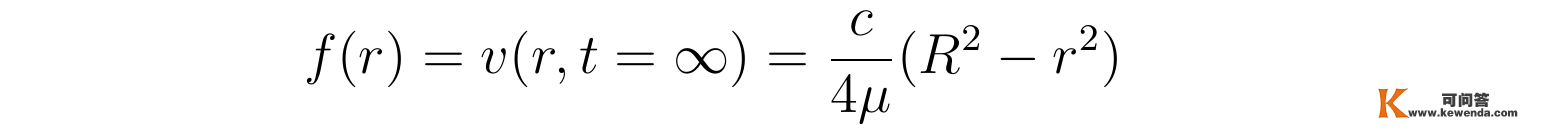
那么函数f(r)称心稳恒层流方程：

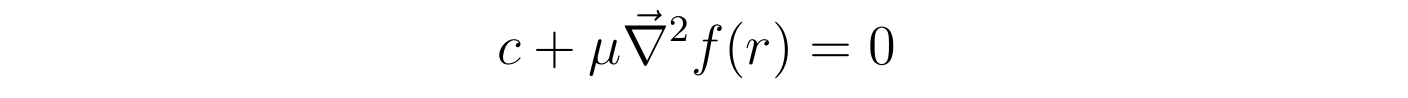
阐发完流速散布的渐停止为后，能够将含时流速合成成如下形式：

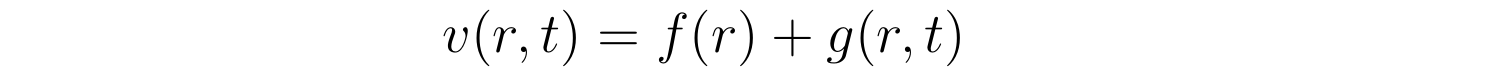
此中函数g(r,t)具有渐停止为g(r,t=∞）=0 。

将该形式的速度散布代进含时速度散布方程，能够操纵f(r)所称心的方程将含时方程进一步化简为：

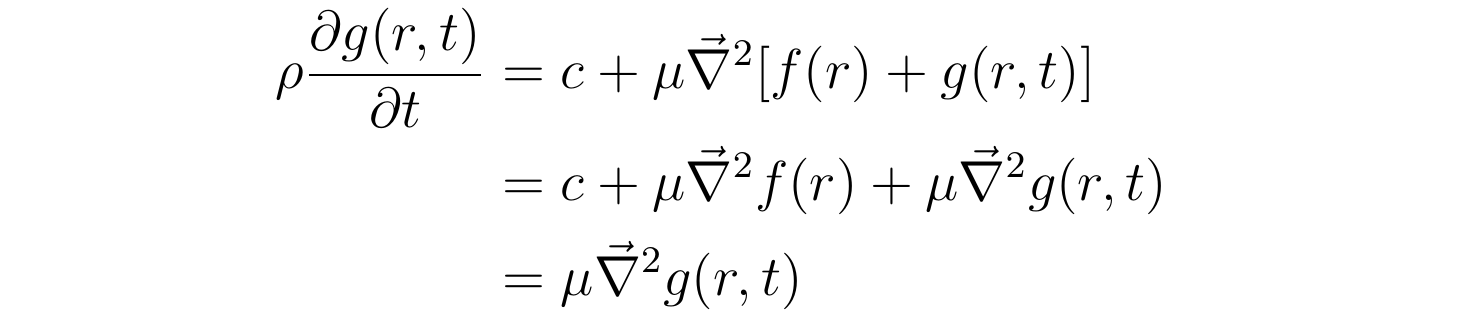
为了后续书写的简洁，那里定义参数ν为：

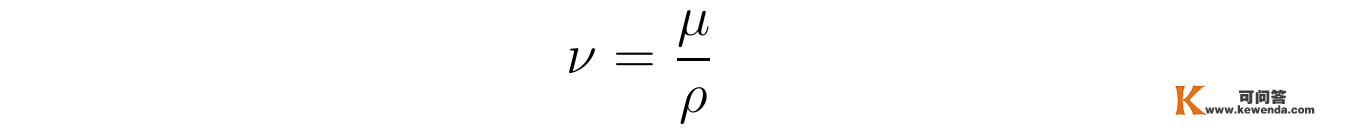
那么函数g(r,t)所称心的方程可写成愈加紧凑的形式：

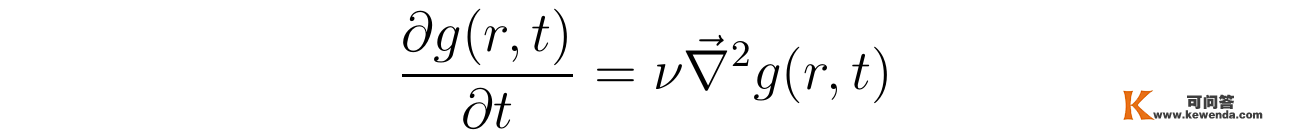
（张向阳阐发流速的渐停止为以化简含时NS方程）

先前的曲播课也碰着类似形式的方程，能够利用别离变量法来求解方程。详细是将函数g(r,t)的时间与空间分隔：

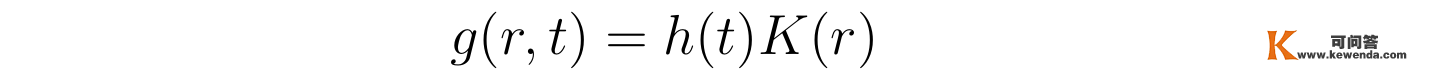
并代进函数g(r,t)所称心的方程，两边再同时除以g(r,t)得到：

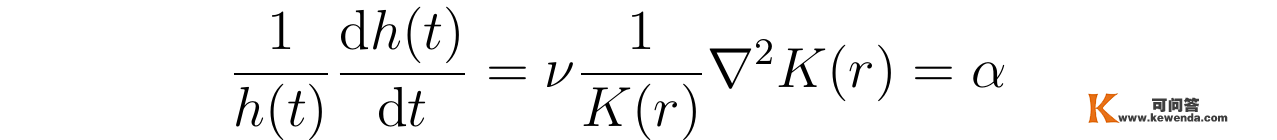
此中，第一个等号右边只含有变量t而右边只含有变量r，那表白等号左（右）边与变量t与r都无关，是一个常数，所以最初一个等号令该常数为参数α 。于是，可用参数α表达函数h(t)称心的方程以及方程的解：

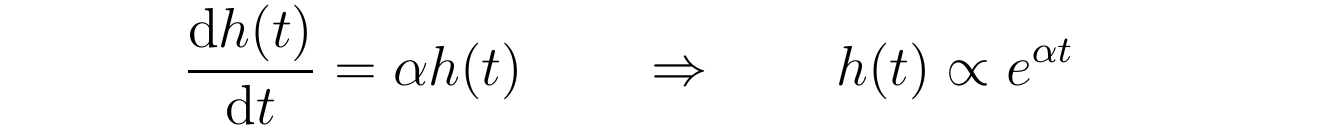
此中因为函数g(r,t)具有渐停止为g(r,t=∞）=0 ，所以α小于零，即-α0。

而用参数α表达函数K(r)称心的方程则为：

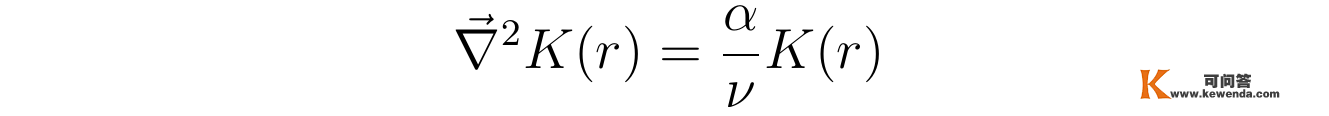
操纵拉普拉斯算子在柱坐标系下的表达式，可将上述方程写成如下常微分方程：

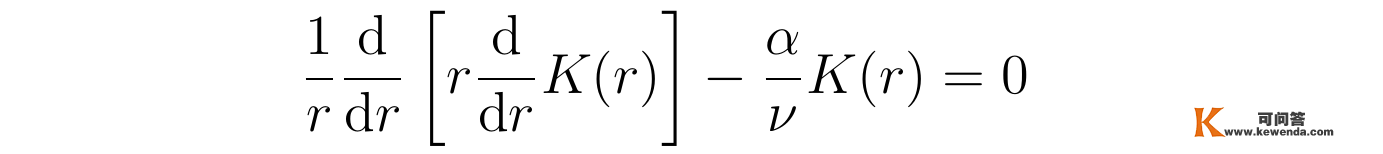
整理此中关于r的导数，详细写成二阶线性齐次微分方程的形式：

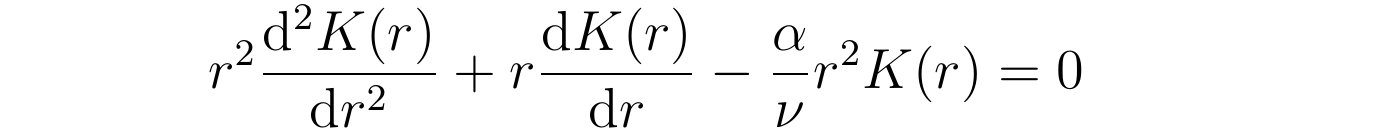
为了将无关系数吸收掉，并因为-α0，可定义参数x为：

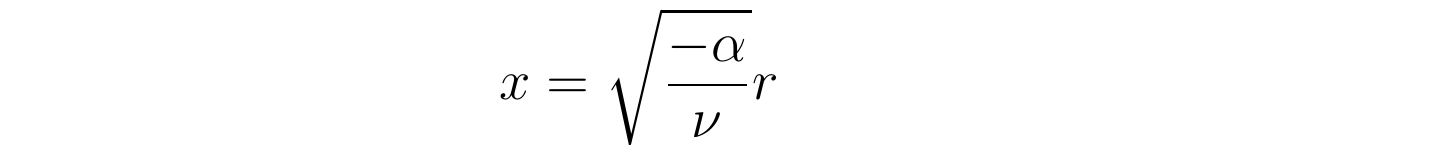
那么方程可进一步改写为愈加简洁的形式：

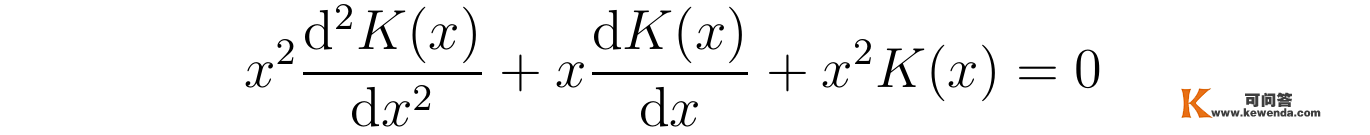
需要阐明的是，此中K(x)关于x与K(r)关于r并非统一个函数，严厉来讲K(x)关于x的函数是K’(x)=K(r)=K(x√(-ν/α) ），只不外那里为了书写便利不消K’(x)而仍然用K(x)。

在数学物理办法中有十分闻名并被研究深入的n阶贝塞尔方程：

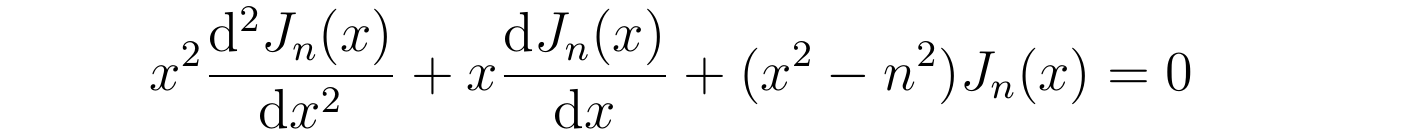
将K(x)所称心的方程与n阶贝塞尔方程做比照，能够发现K(x)所称心的方程恰是0阶贝塞尔方程。

（张向阳别离变量求解含时方程并得到贝塞尔方程）

操纵递推公式求得贝塞尔函数 根据鸿沟前提确定流速散布

为了最末得到含时的流速散布，张向阳摘用微分方程的幂级数解法，将函数K(x)展开为自变量x的幂级数：

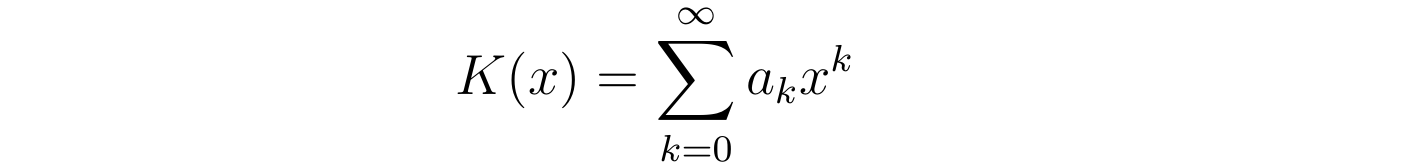
将K(x)的幂级数形式代进上述0阶贝塞尔方程中，交换求导与乞降挨次后得到：

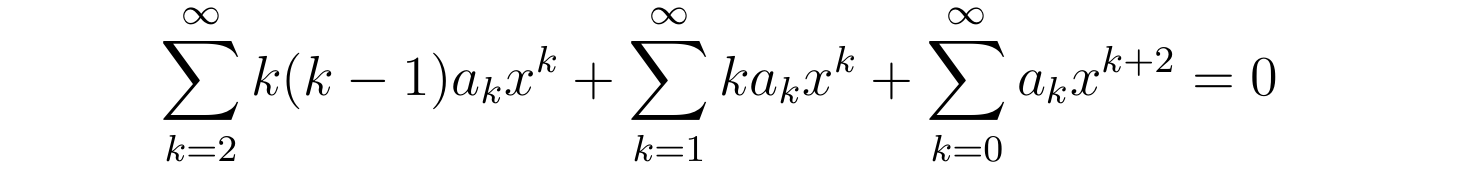
进一步将关于x不异幂次前的系数合并得到：

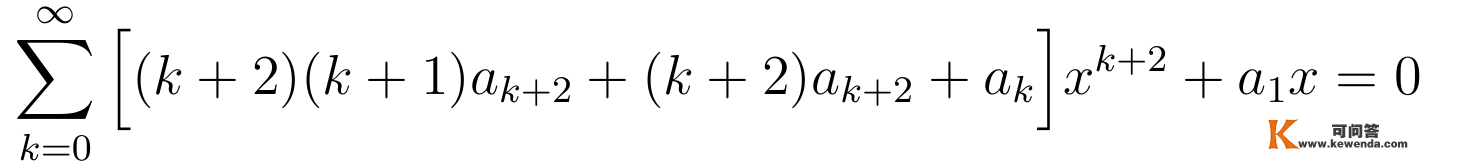
因为x能够取肆意值，那要求任何幂次前的系数都为零：

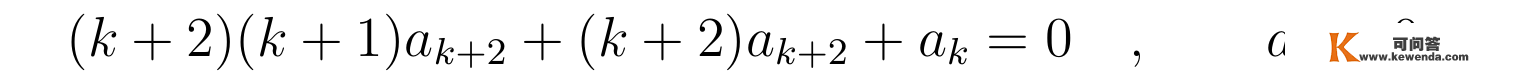
上式逗号右边的等式表白K(x)的展开系数的k+2项与k项有递推关系：

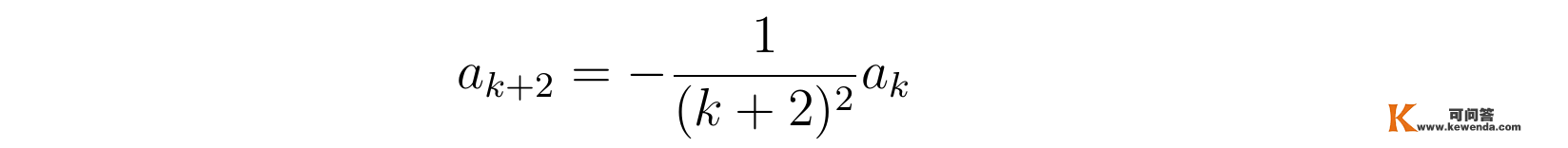
又因为a1=0，根据递推关系知a3反比于a1，即a3=0，又因为a5反比于a3，所以a5=0，同理可得展开系数a的所有奇数项都为零，只要偶数项可能不为零。若ak不为零，那么递推关系可写成：

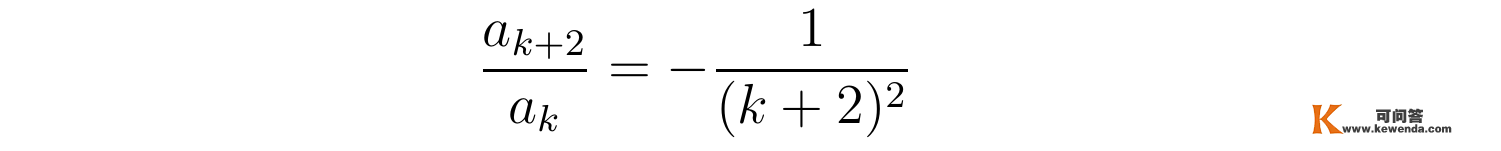
于是肆意偶数项与a0的关系为：

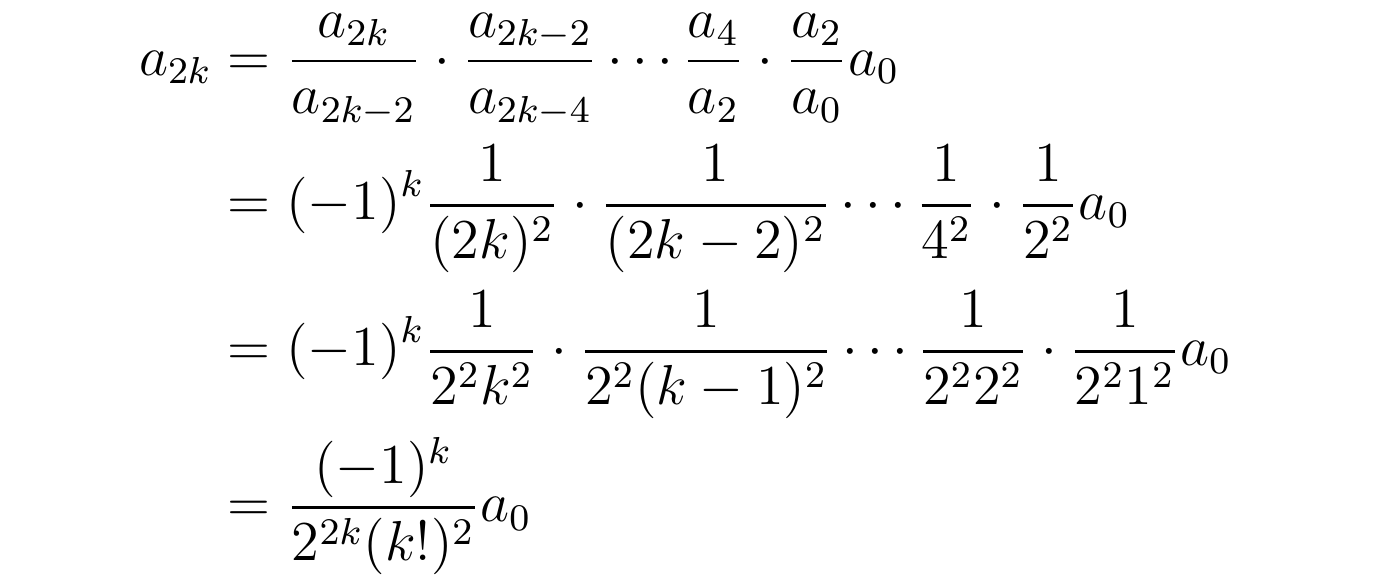
将上述求得的展开系数带回K(x)的级数展开表达式，可得0阶贝塞尔方程的解：

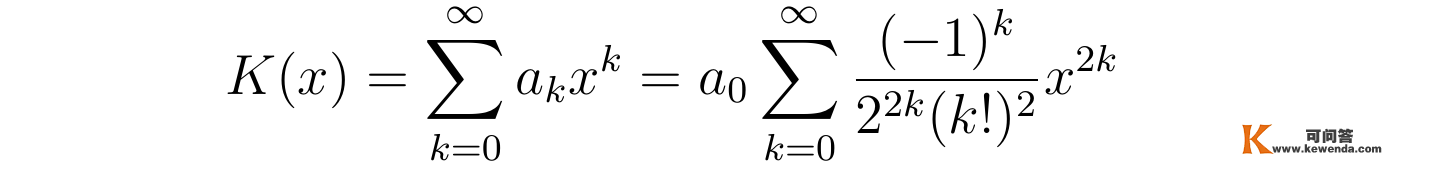
（张向阳推导出贝塞尔方程级数解法的递推公式）

数学家已足够研究过肆意阶数的贝塞尔方程，0阶贝塞尔函数的此中一个解，即第一类贝塞尔函数为：

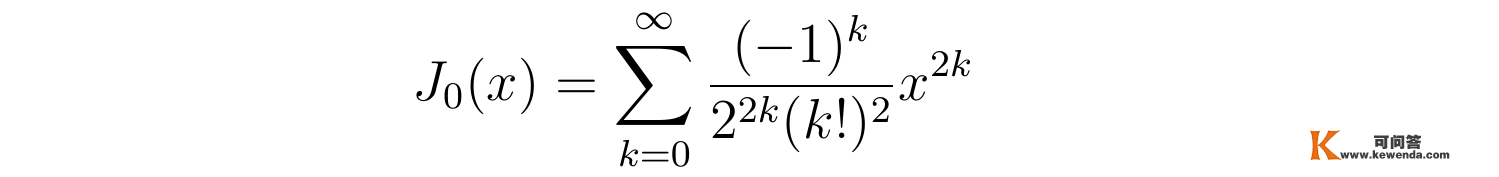
重视到二阶线性齐次微分方程的解能够相差肆意常数的倍数，若将K(x)的幂级数中的第零项的系数a0取为1，那么用幂级数展开与递推公式得到的解，恰是第一类贝塞尔函数。即一般情状下有：

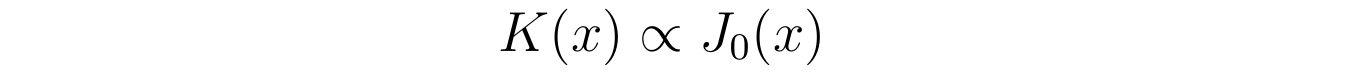
进一步连系x与α的关系式以及h(t)的表达式可得函数g(r,t)反比于如下形式：

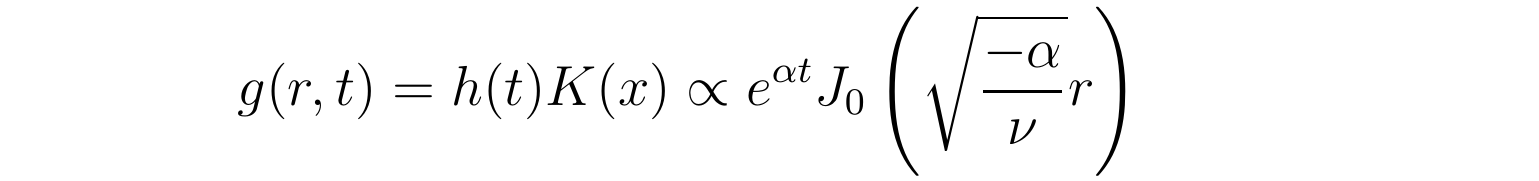
重视到上式中参数α的取值具有肆意性，关于差别的α，上式都是方程的解。而g(r,t)称心的微分方程是线性齐次微分方程，所以那些解的叠加仍然是方程的解。用下标i来标识表记标帜差别值的参数α，那么愈加一般的解可写为：

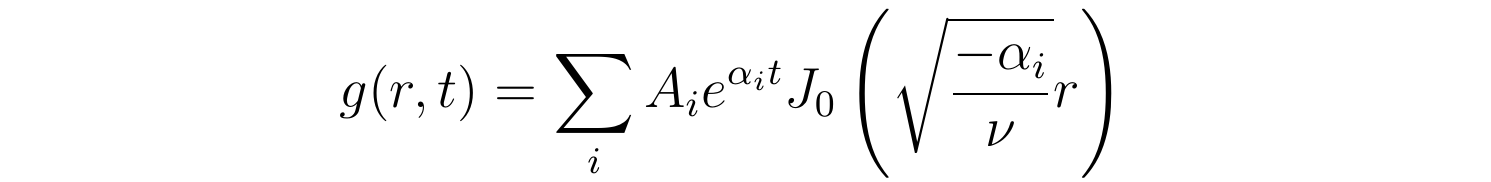
此中，Ai是与变量r和t都无关的常数。

连系函数f(r)与g(r,t)的表达式，流速散布具有如下形式：

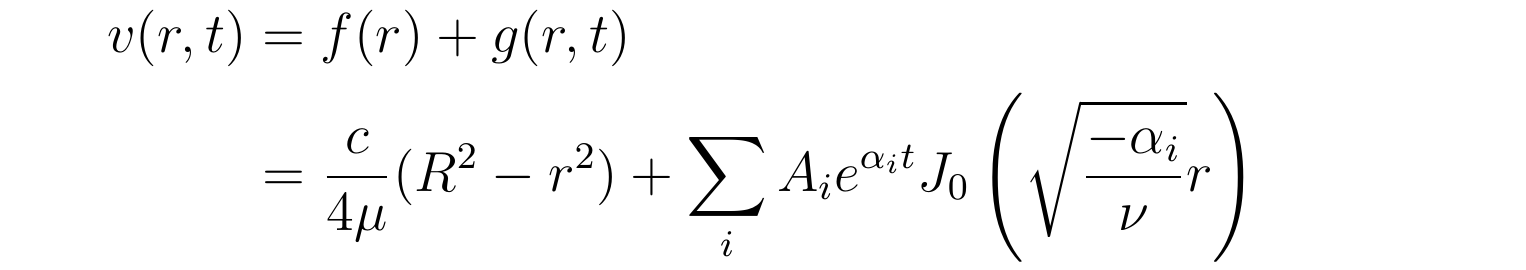
为了进一步限制参数α的值，张向阳考虑不滑动鸿沟前提，即流速在圆管内壁r=R处恒为零：

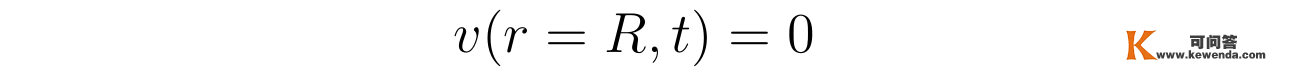
在此鸿沟前提的限造下，关于流速散布函数，其第一项f(r)主动称心f(r=R)=0；而第二项中，因为g(r,t)中关于差别的i有着差别的含时e指数函数，那就要求对每一个i，在r=R处都称心0阶贝塞尔函数取值为零

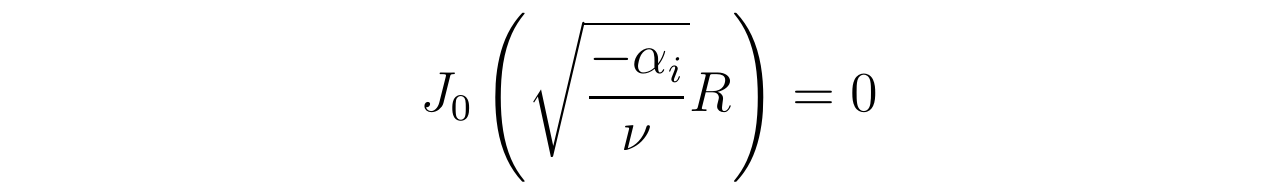
设λi是0阶第一类贝塞尔函数的第i个零点，即J₀(λi)=0，那么根据上式显然有：

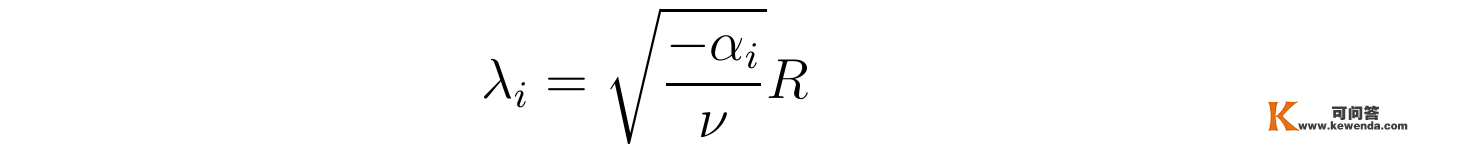
重视到贝塞尔函数有无限多个零点，于是可求得α的取值为：

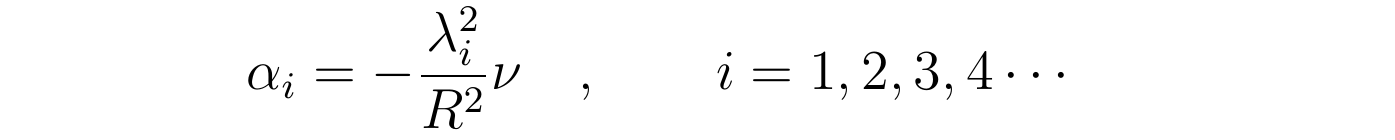
有了参数α的详细取值，流速散布可用贝塞尔函数的零点λi写成愈加详细的形式：

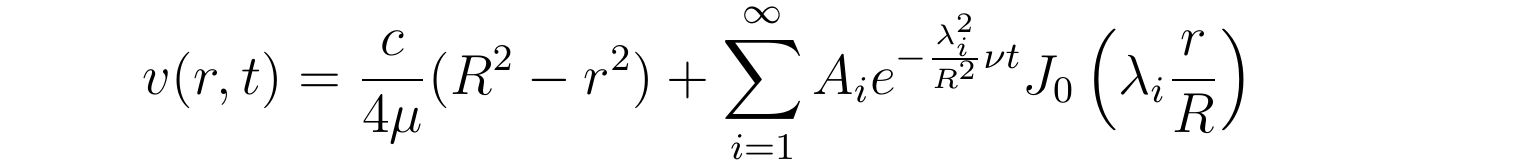
为了进一步将叠加参数求出来，张向阳定义了如下新变量以便利后续计算与推导：

如许就能够将速度散布中无关紧要的系数cR^2/4μ提取出来，得到如下大括号中愈加简洁的形式：

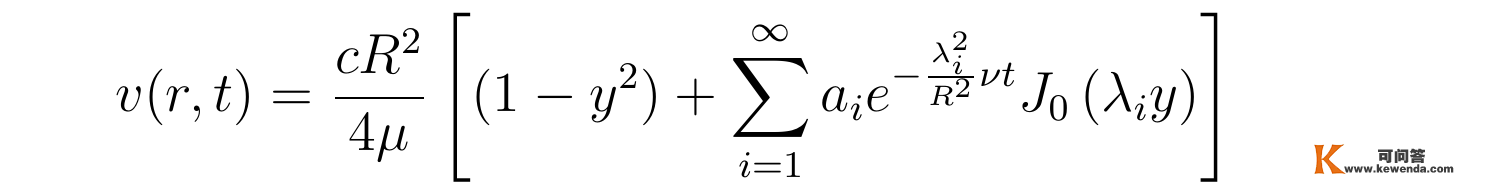
除了不滑动鸿沟前提，那里还有另一个鸿沟前提，是方程的初始前提，即t=0时刻流速处处为零：

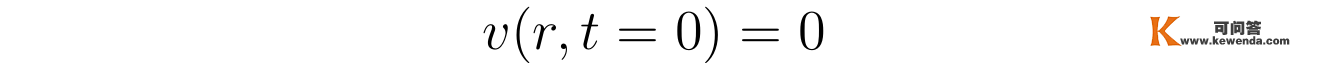
将上述新变量表达的流速散布代进上述鸿沟前提中得到：

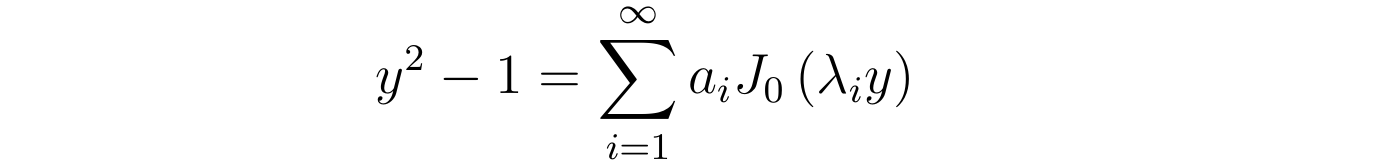
上式表白，叠加系数ai是函数y^2-1用0阶贝塞尔函数展开后的各项系数，那种体例展开得到的级数称为傅里叶-贝塞尔级数。详细若何得到级数各项的展开系数，请见下回合成。

（张向阳根据鸿沟前提引出傅里叶-贝塞尔级数）

据领会，《张向阳的物理课》于每周周五、周日中午12时在搜狐视频曲播，网友能够在搜狐视频“存眷流”中搜刮“张向阳”，看看曲播及往期完全视频回放；存眷“张向阳的物理课”账号，查看课程中的“常识点”短视频。此外，还能够在搜狐新闻APP的“搜狐科技”账号上，阅览每期物理课程的详尽文章。