圆管中粘性不成压缩流体的流量与什么有关?《张向阳的物理课》推导泊肃叶定律
若何求解简单情状下的纳维尔-斯托克斯方程?圆管中粘性不成压缩流体的流量与什么有关?《张向阳的物理课》第一百一十一期在12月25日12时开播,搜狐开创人、董事局主席兼CEO张向阳坐镇搜狐视频曲播间,先给网友们复习了纳维尔-斯托克斯方程,然后假定圆柱形管中流体做稳恒层流运动,并化简纳维尔-斯托克斯方程,继而解得圆管中流体的流速的抛物线散布,进一步根据流速与半径的关系推导出泊肃叶定律,最初讲解该定律的一些利用。
研究圆管中的粘滞流体 化简纳维尔-斯托克斯方程
在之前的曲播课程中,张向阳介绍了流体力学中的根本概念,并推导了纳维尔-斯托克斯方程:
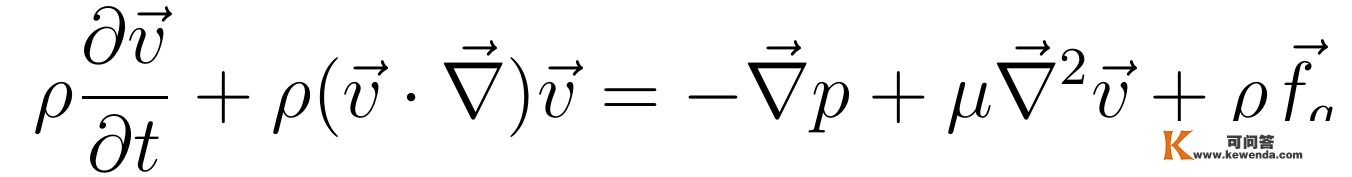
此中,μ是流体的粘滞系数,它描述液体的内摩擦属性。纳维尔-斯托克斯方程反映了不成压缩粘性流体活动的根本力学法例,它是一个非线性偏微分方程,一般情状下很难求解,只在某些简单特例下才气求得其切确解。那节课将介绍一个具有高度对称性的例子,并求解该情状下的纳维尔-斯托克斯方程。
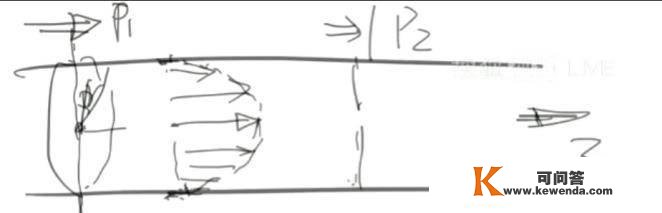
展开全文
如上图所示,流体在一个半径为R的圆柱形管中活动,以管中心轴为z轴,成立柱坐标系。雷诺数Re=ρvd/μ是表征流体活动情状的无量纲数,此中d是圆柱管道的曲径。雷诺数小于2000时,粘滞力对流场的影响大,流场中流速的扰动会因粘滞力而衰减,流体活动不变,构成稳恒层流;反之,当雷诺数较大时,流体活动较不不变,随便构成湍流。
假设流体雷诺数较小,流体处于稳恒活动的形态,并认为流体只要沿着z标的目的的速度,且具有绕z轴的扭转对称性。那么因为流体不成压缩,由流量守恒可知速度与坐标z无关,柱坐标系中流体的速度场能够写成:
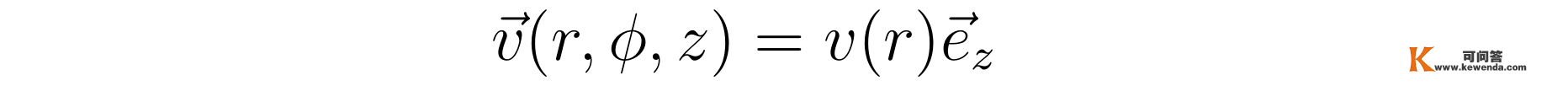
此中,e_z是沿z轴正标的目的的单元向量。
因为流速与时间无关,在不考虑重力场的情状下,纳维尔-斯托克斯方程能够写成稳恒形式:
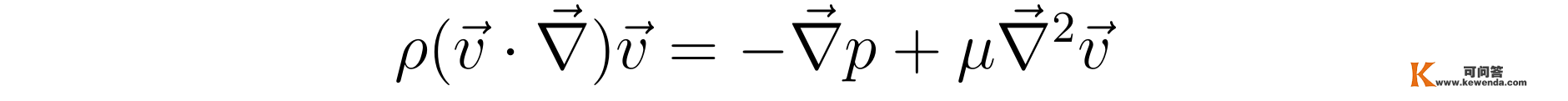
张向阳先阐发上述方程等号右边的项。在柱坐标系中三维导数算符能够表达为:
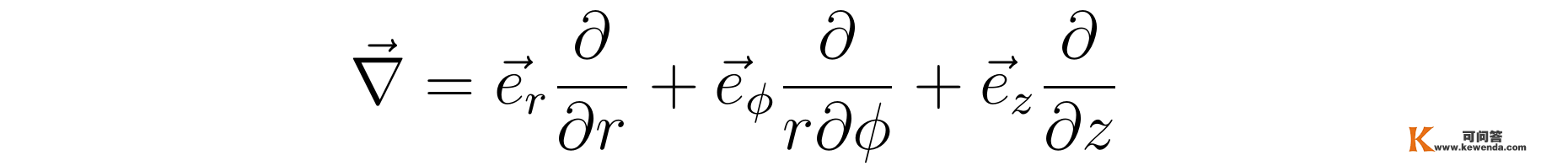
由导数算符的柱坐标形式,连系速度场在柱坐标下的表达式v(r,Φ,z)=v(r)e_z,能够得到:
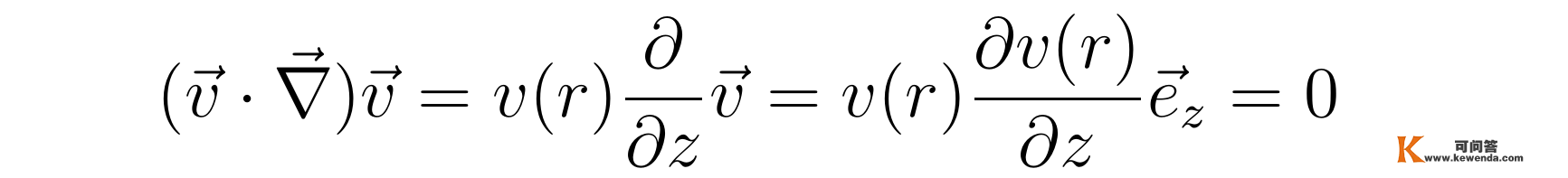
于是,前述稳恒情状下的纳维尔-斯托克斯方程能够陆续化简成:
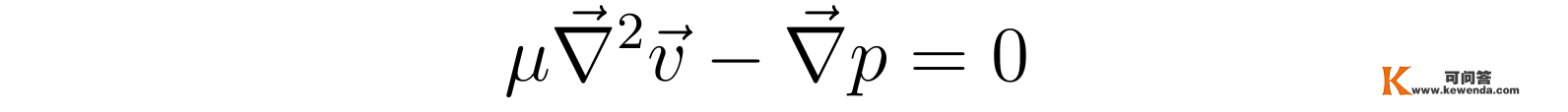
为了进一步化简方程,张向阳接着阐发拉普拉斯算子在柱坐标系下的表达式:
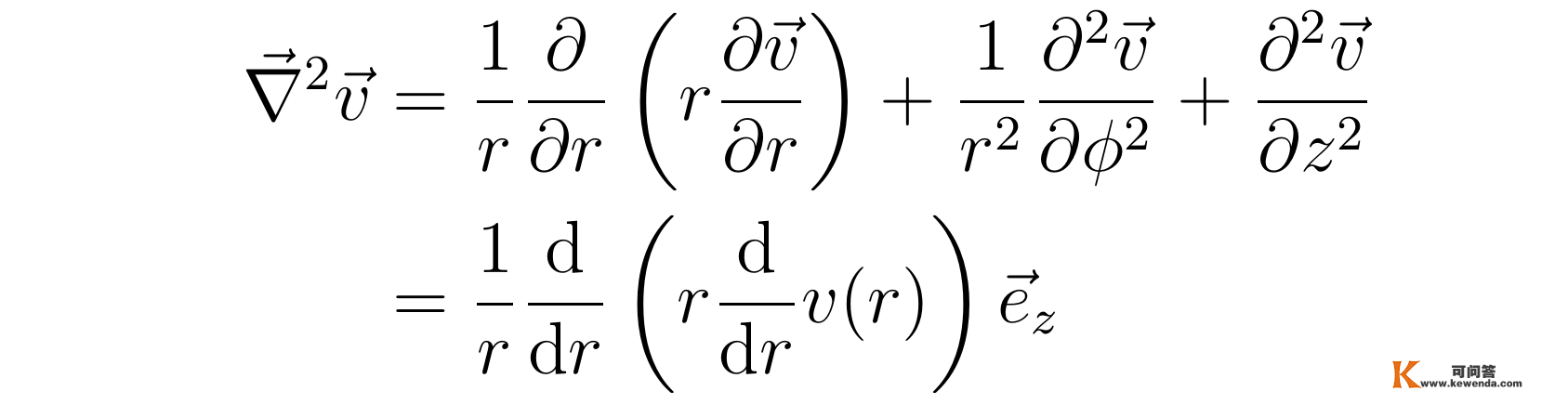
此中,最初一个等号操纵了速度场与柱坐标Φ和z无关的性量。重视到方程中含有拉普拉斯算子的项μ▽²v只要z重量不等于零,阐明方程中的另一项▽p也只要z重量不为零,x重量与y重量都为零,即∂p/∂x=∂p/∂y=0,由此进一步可得∂/∂x(∂p/∂z)=∂/∂z(∂p/∂x)=0与∂/∂y(∂p/∂z)=∂/∂z(∂p/∂y)=0,那阐明∂p/∂z与x和y都无关。关于z重量,纳维尔-斯托克斯方程能够写成:
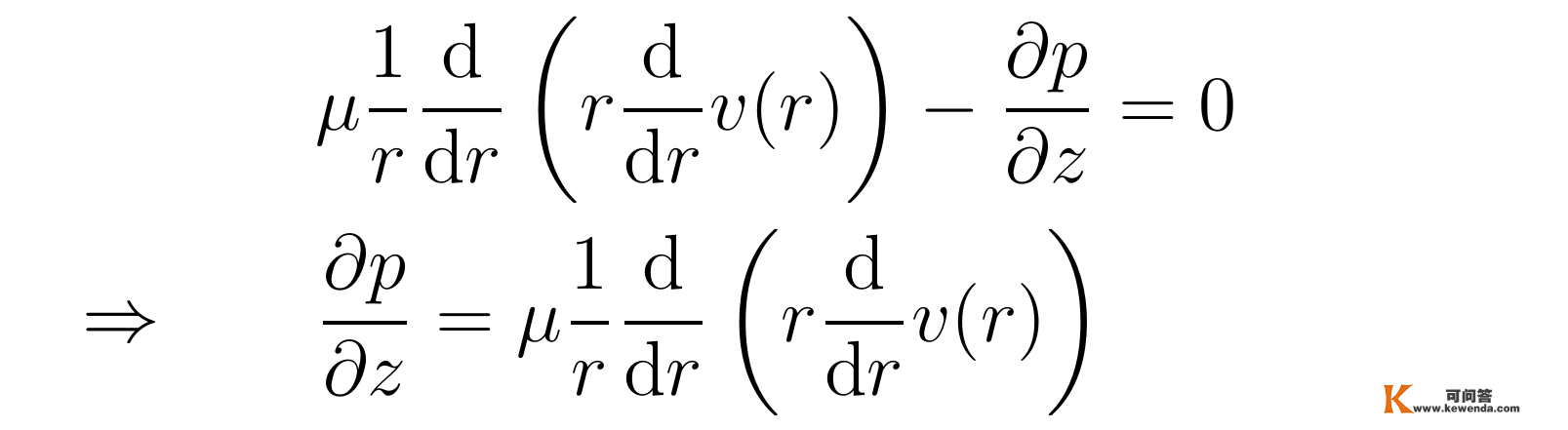
重视到v只与r有关,与z无关,那阐明∂p/∂z与z无关,连系前述∂p/∂z与x和y都无关的性量,可知∂p/∂z在整个圆柱管中都是一个常数,于是令∂p/∂z=-c,此中负号表达压强跟着z轴减小之意。
于是,纳维尔-斯托克斯方程最末化简成了十分简单的微分方程:
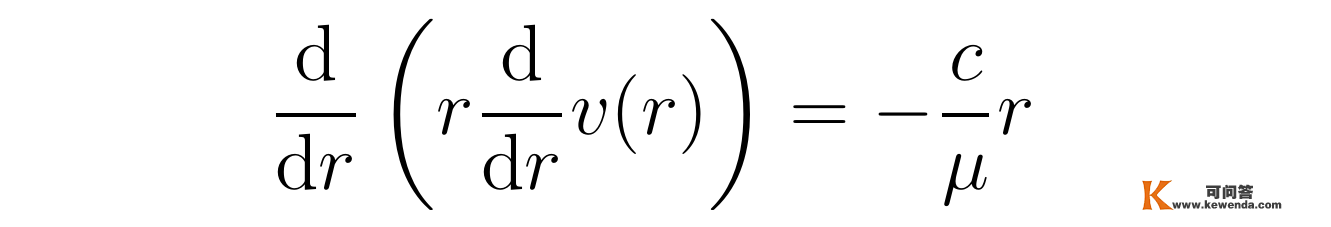

(张向阳化简圆管中层流流体的纳维尔-斯托克斯方程)
求解纳维尔-斯托克斯方程 推导泊肃叶定律
上述微分方程能够间接两边积分得到方程的解,但根据方程摆布两边关于r的幂次的阐发,以及圆管流量有限的事实,随便揣测,方程的解应具有如下简单的形式:
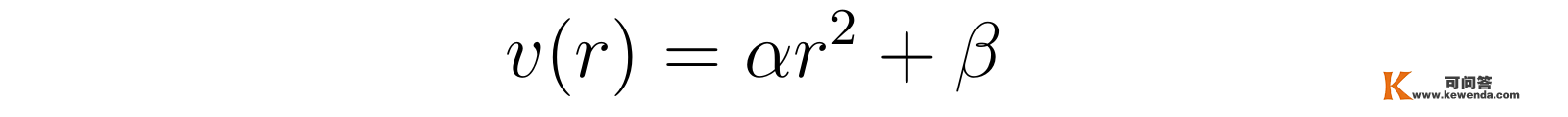
将该形式的解带回方程中可求得参数α的值:
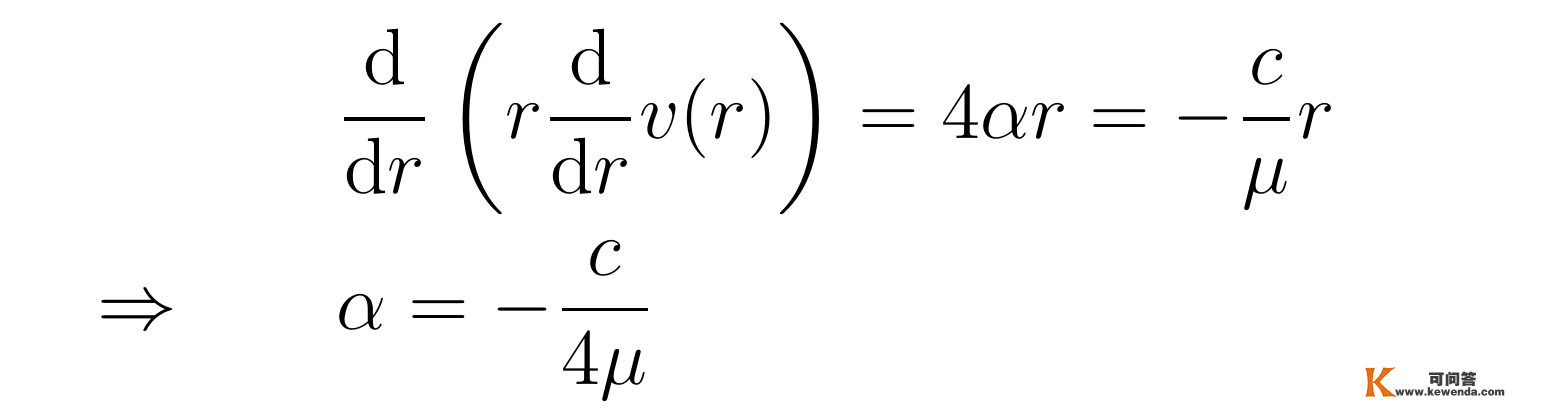
至于参数β,则需要引进鸿沟前提。那里假定不滑动鸿沟前提,即管壁r=R处流体流速为零,那么能够解得参数β为:

于是,流体流速v与半径r呈抛物线型关系:
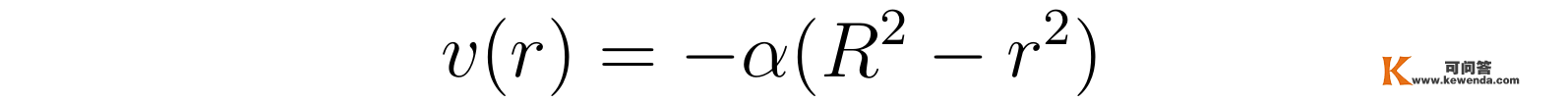
解得了流速场后,张向阳进一步计算了单元时间内流过肆意截面的流体量量Q:
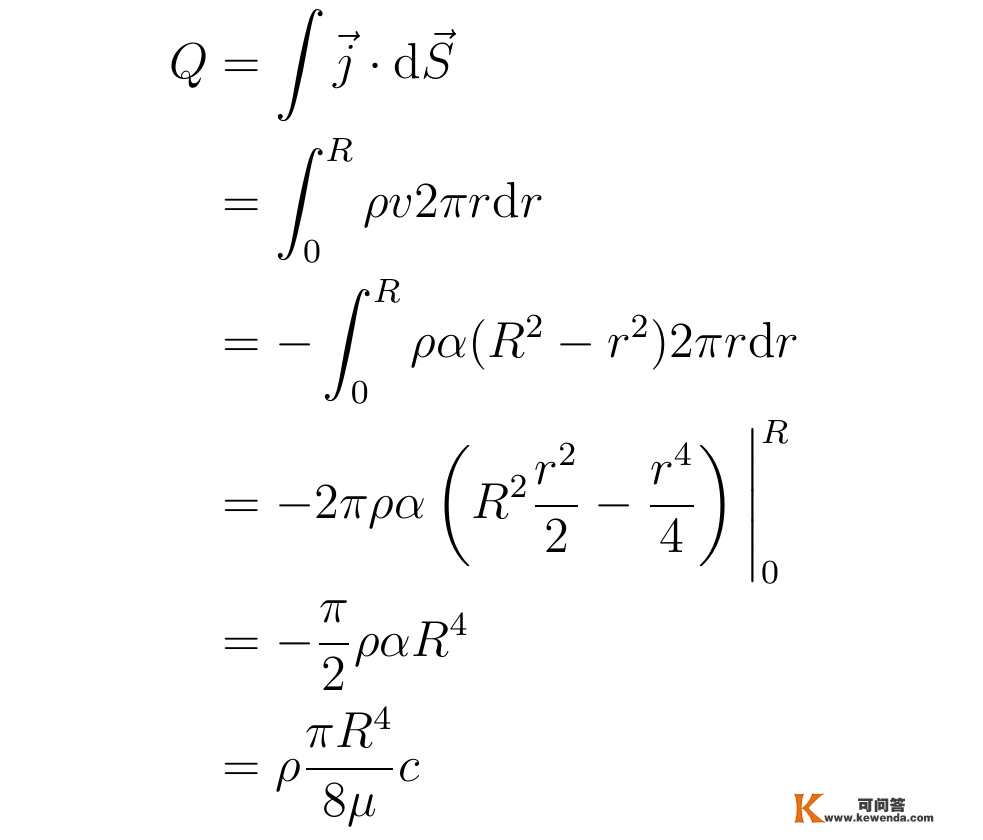
此中,j=ρv是量量流密度,别的最初一个等号已将参数α=-c/(4μ)代进公式中。关于不成压缩流体,人们凡是用体积流量来描述流体活动情状,单元时间流过截面的流体体积为其量量除以密度:
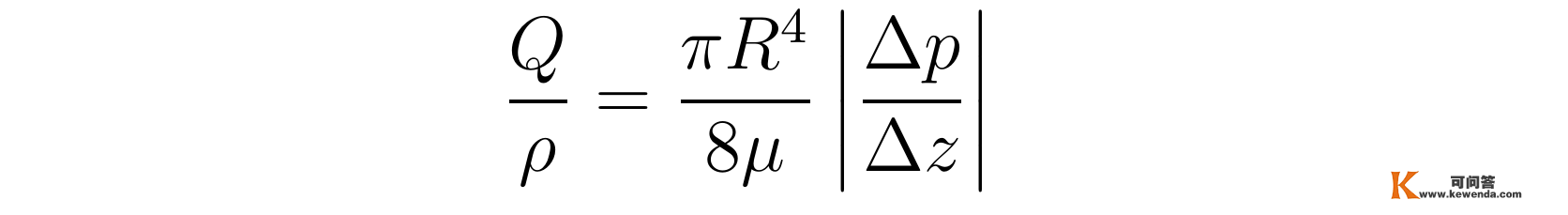
此中,已经将常数c详细写成一段间隔|Δz|两头的压强差|Δp|与该段间隔的比值|Δp/Δz|的形式。上述公式所描述了流量与流体压强和圆管参数之间的关系,那就是闻名的泊肃叶定律。
泊肃叶定律显示了粘性流体的特征,一般情状下人们可能会从曲看上认为流体流量与圆管的截面积成反比,即与圆管半径R^2成反比,但现实上粘性流体的速度关于半径并非一个常数——圆管中心流速大、边沿流速小,且圆管半径越大,中间的流速也越大,招致最末成果是流量与R^4成反比。
做为一个利用案例,以上法例可用于研究血管中血液的活动。例如关于动脉粥样硬化的病人,其血管中因为堆积了脂肪或其它杂量,血管有效半径减小,因为在压强稳定的情状下贱量与R^4成反比,即血流关于R十分灵敏。例如R减小成1/2 R,血流量将急剧减小为本来的1/16,血流量不敷会对人体产生严峻后果。而假设要加大血流量,则需要增加血压,那又可能招致高血压等安康问题。
除此之外,泊肃叶定理还有良多其它利用,例如打吊针时为了使吊瓶里的液体更快地流进人体,能够进步吊瓶,操纵重力增加流体两侧的压强差,使得流量加大。也恰是因为泊肃叶定律在医学上的各类利用,那个重要的物理法例更先是由法国医生泊肃叶发现的。

(张向阳求解纳维尔-斯托克斯方程并推导泊肃叶定律)
据领会,《张向阳的物理课》于每周周五、周日中午12时在搜狐视频曲播,网友能够在搜狐视频“存眷流”中搜刮“张向阳”,看看曲播及往期完全视频回放;存眷“张向阳的物理课”账号,查看课程中的“常识点”短视频。此外,还能够在搜狐新闻APP的“搜狐科技”账号上,阅览每期物理课程的详尽文章。
