香蕉球的物理原理是什么？《张向阳的物理课》证明浮力定律与伯努利定理

足球角逐中的香蕉球是怎么回事？它为什么可以拐弯？怎么严厉证明阿基米德浮力定律与伯努利定理？12月4日12时，《张向阳的物理课》第一百零七期开播，搜狐开创人、董事局主席兼CEO张向阳坐镇搜狐视频曲播间，简要回忆了上一次曲播课所介绍的流体力学常识，然后借助矢量阐发以及微元阐发法，证明了阿基米德浮力定律；紧接着推导了标量场的微分公式，并借助它胜利证明了伯努利定理。

物体拆成柱状微元 压差乞降得到浮力

课程一起头，张向阳简要回忆了上一次曲播课程介绍的常识，包罗压强、稳恒活动等概念，还有帕斯卡原理、浮力定律等物理法例。张向阳强调，之前所介绍的常识都是比力初步的，好比浮力定律，只是阐了然它在柱形体等规则外形的情状下成立，而没有一般性地对肆意外形赐与证明。在此次曲播课中，张向阳对浮力定律、伯努利定理都做了严厉证明。

根据前次曲播课的成果，密度为ρ的不成压缩静行流体在重力场中的压强称心

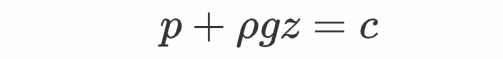
此中的c表达与位置、时间无关的常数；z是曲角坐标系的第三个坐标，坐标轴的正标的目的竖曲向上。上式能够改写为p=-ρgz+c。

察看一个淹没在流体中的肆意外形的物体（注：此处的推导颠末恰当修改也可用于不完全淹没的物体），示企图如下：

展开全文

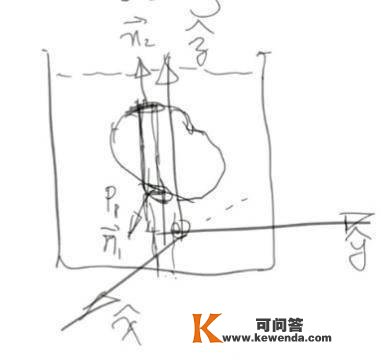
如图所示，取物体的一个柱形微元，其横截面大小为dS_{xy}；下底面面积为ds1，单元法向是n1；上底面面积为ds2，单元法向是n2。用i，j，k表达三个坐标轴的单元向量，那么那个柱形微元遭到的流体压力的z重量为

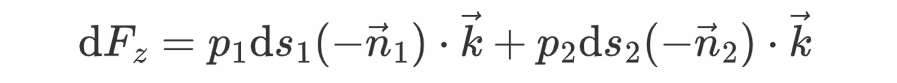
式中n1与n2前的负号来自于压力标的目的与外表法向的标的目的相反。因为

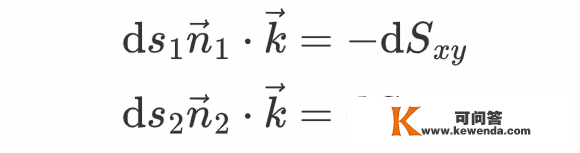
将其代进前式可得

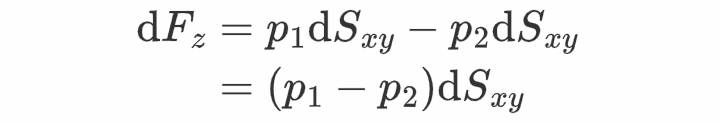
将所有柱形微元遭到的压力图和，借助前面介绍的压强公式p=-ρgz+c，可得

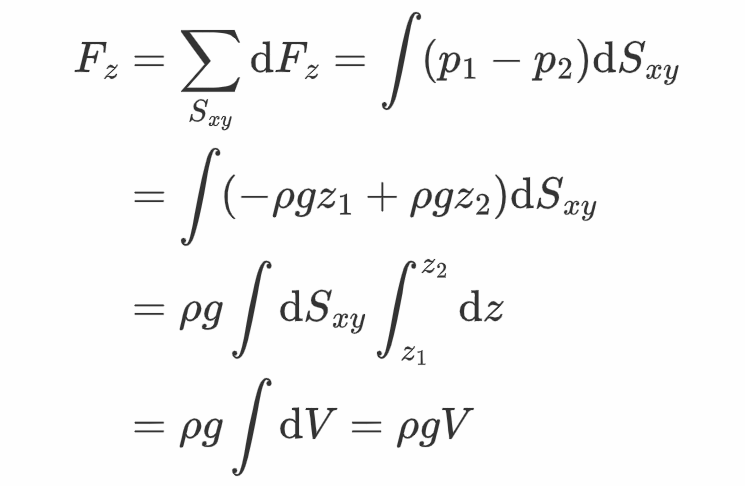
可见Fz的标的目的是竖曲向上的，大小等于那个物体排开的水的重力大小。但是，阿基米德定律还要求物体遭到的浮力沿x与y标的目的的重量为零，因而还需要证明那个物体遭到的流体压力在x、y标的目的为零。不失一般性，只需证明x标的目的的重量为零即可。与前面的推导类似，只不外此次需要取平行于x标的目的的柱形微元，最初得到

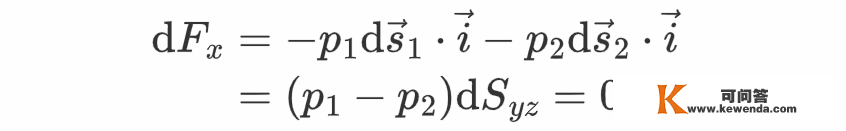
最初的等号是因为统一程度面的压强相等，即p1-p2 = 0。

至此，阿基米德浮力定律的证明就已经完全了。

（张向阳证明阿基米德浮力定律)

阐发压力体密度 推导标量场微分式

在上一次曲播课程中，张向阳借助特定指向的微元阐了然压强的负梯度为压力的体密度，因而，压强代表着压力密度的势。在那一次曲播课程中，对此论断给出了更详尽的证明。

取一立方体微元，微元各边平行于各坐标轴。设微元沿x标的目的的横截面面积为ΔA，微元占据的x标的目的的坐标范畴为[ x, x+Δx ]，那么微元遭到的x标的目的的压力为

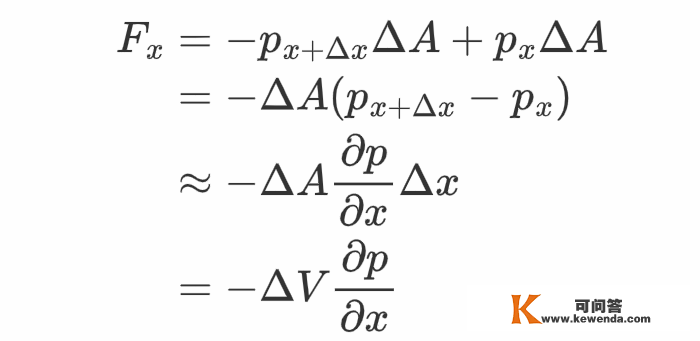
此中ΔV = ΔA·Δx是微元的体积。由此可知压力体密度在x标的目的的重量为

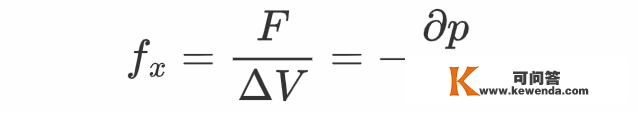
基于同样的阐发，能够得到其它两个标的目的的压力体密度别离为

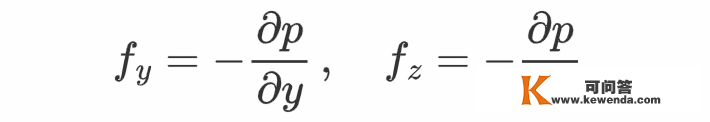
综合那些成果，即可得到压力体密度

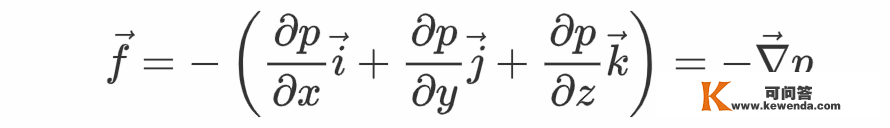
可见，压强确实是压力体密度所对应的势。那个成果其实是阿基米德浮力定律的微分形式，那种联络；类似于电磁学中“电场的散度等于ρ/ε0”与高斯定理的联络。

阐发完压力体密度，起头介绍起标量场在无限小间隔上的差。因为压强是一种特殊的标量场，且与当前课程内容间接相关，因而张向阳间接利用压强来停止阐发。假设空间上两点的间隔为

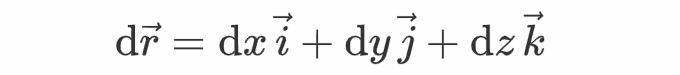
那么

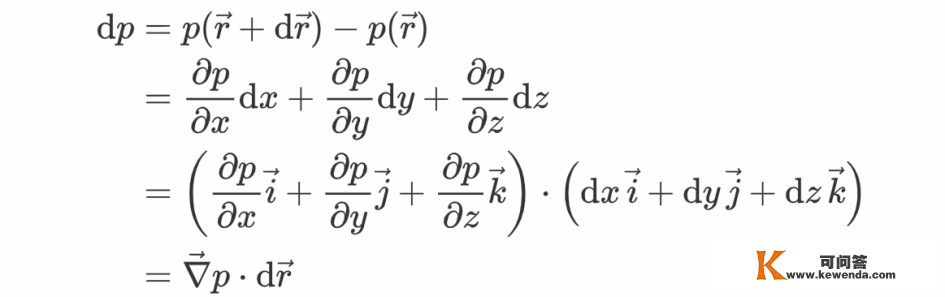
可见，标量场的微元可用它的梯度与空间间隔微元的点乘来表达。张向阳介绍说，此成果将在接下来对伯努利定理的证明顶用到。

阐发能量沿途径的改变量 证明伯努利定理

在上一次曲播课程中，根据压强是一种势，借助能量守恒定律写出了伯努利定理：

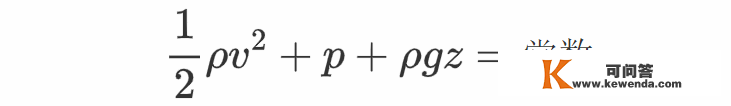
但是其时并没有对此成果停止严厉的证明，并且此中的常数为什么仍依靠于空间坐标，那个问题也没有得到解答。为了彻底处理那些问题，张向阳定义

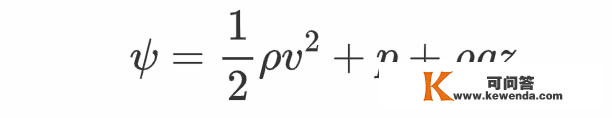
为了凸起问题的核心，在接下来的推导中漠视了此中的重力势能项ρgz，不外，加上那一项时，下面的推导过程仍然成立。

假设某处的流体微元速度为

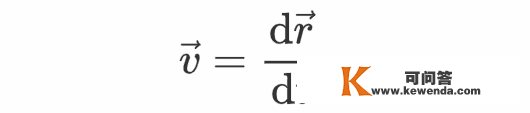
那么矢量dr将是那个流体微元的前进标的目的。考虑在dr间隔下的ψ改动量，根据前面的阐发，此改动量能够写成梯度与dr的点乘：

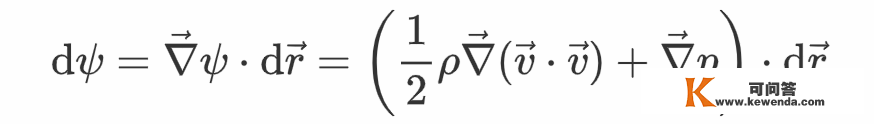
根据矢量微积分的公式

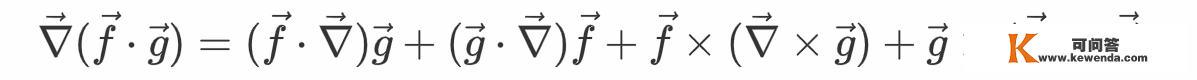
将此中的f与g都取为v，能够得到

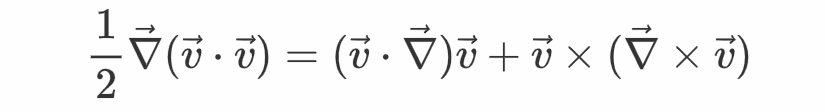
将此成果代进dψ的式子中即有

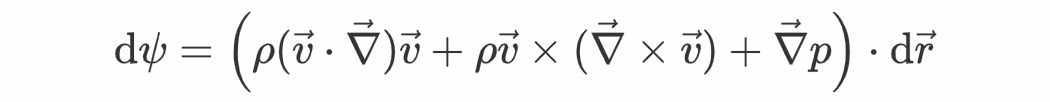
另一方面，重视到速度v是一个矢量场，它是依靠于空间与时间的，因而微元的加速度为

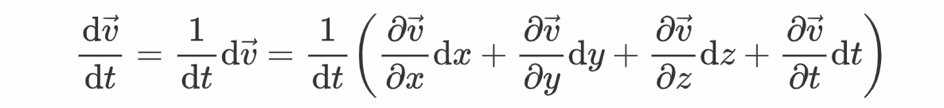
因为

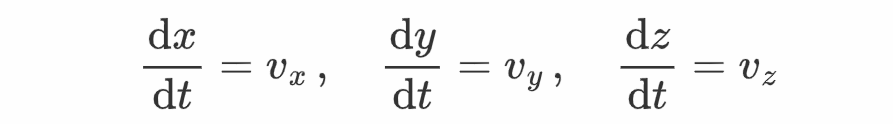
且流体稳恒活动，其速度散布不依靠于时间，有

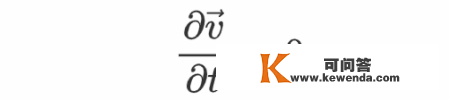
所以，微元的加速度能够写为

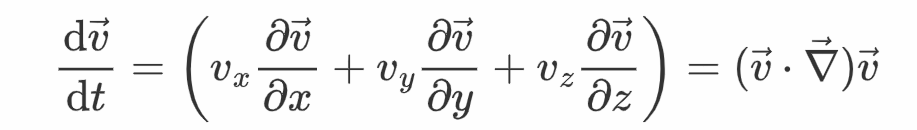
因而，dψ的式子中右边大括号内的第一项能够借助上式来替代，于是得到

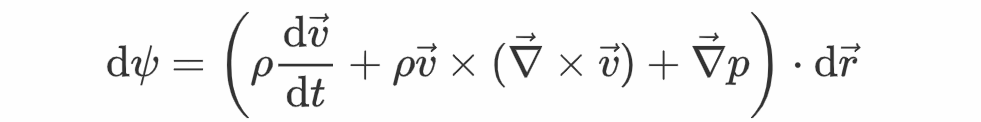
漠视重力感化，根据牛顿第二定律，微元加速度与密度的乘积必需等于微元遭到的压力体密度，也就是压强的负梯度：

因而dψ能够简化为

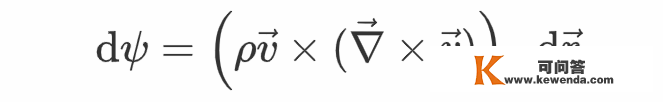
张向阳强调，固然关于不成压缩流体，其速度的散度为零，但速度的旋度纷歧定为零，设

因为矢量dr平行于速度v，故dr垂曲于v×α，从而dr与v×α的点乘等于零。由此可得，dψ=0。那阐明，沿着速度场前进时，ψ的改动量等于零，换言之，ψ在流线上连结为统一个常数。

(张向阳证明伯努利定理)

那里的推导只证明了ψ沿流线连结恒定，但是差别流线上的ψ可能是纷歧样的。不外关于一些特殊情状，ψ在整个空间上都等于统一个值。好比在水库上开一个小口，让水不变地活动下来，在那种情状下，因为水库里的水是静行的，其上的ψ处处相等，又因为伯努利定理规定了流线上的ψ连结恒定，因而流下往的水的ψ也是处处相等的。再如别的一种情状，平流，也就是整个流体以固定的速度朝一个标的目的活动，它的ψ也是处处相等的。

证明了伯努利定理，张向阳用它阐发了足球角逐中香蕉球的成因。足球运发动斜着踢球，会给足球带来必然的角动量，使足球飞出往的同时还绕本身扭转。此时，足球除了因重力招致轨迹弯曲之外，还会因自转招致轨迹弯曲，那就是人们常说的”香蕉球”。

假设球是平飞出往的，且球的角速度垂曲空中向上。漠视球的重力，取跟从球一路平动的参考系，那么空气在此参考系中会朝着相反标的目的不竭活动过往，拜见下面的示企图。

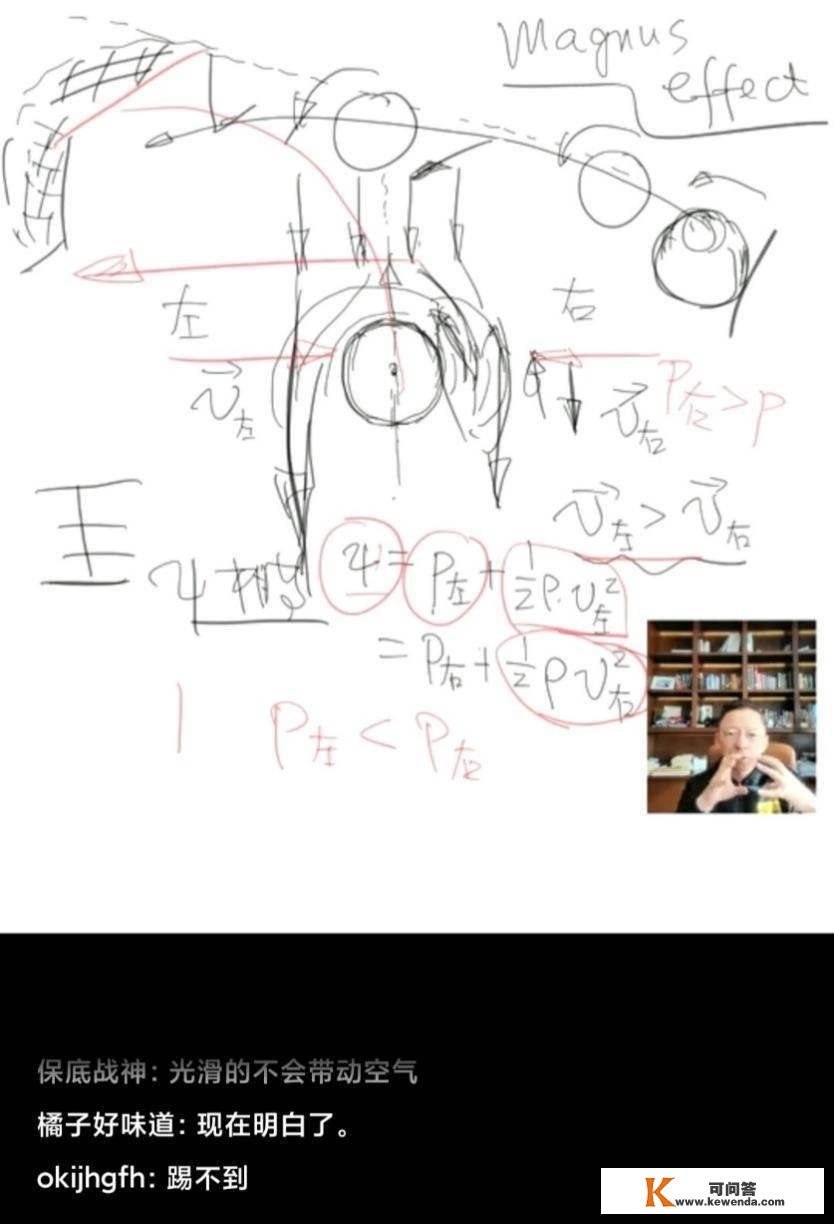
(张向阳阐发香蕉球的成因)

因为球在自转，它会带动四周的空气一路扭转。现实情状是很复杂的，在那里只做了简化阐发。因为空气在远处是平流，因而它的ψ处处相等，于是在球的两边有

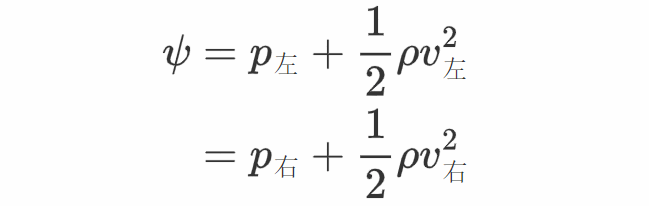
球的自转会招致球两边的空气活动速度纷歧致，球右边的空气会被球的自转带动使得速度更快，球右边的空气则因为球的自转招致速度变慢，因而借助上式能够得到

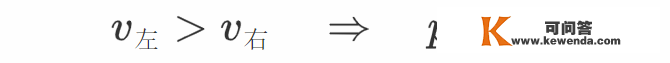
右边的压强高于右边的压强，因而球会遭到一个从右向左的力，从而向左拐弯，那就是香蕉球的成因。

据领会，《张向阳的物理课》于每周周五、周日中午12时在搜狐视频曲播，网友能够在搜狐视频“存眷流”中搜刮“张向阳”，看看曲播及往期完全视频回放；存眷“张向阳的物理课”账号，查看课程中的“常识点”短视频。此外，还能够在搜狐新闻APP的“搜狐科技”账号上，阅览每期物理课程的详尽文章。