流体的微元与微元之间存在摩擦力?怎么定量描述流体的内部摩擦力?考虑了粘滞系数后,流体的运动方程是如何的?《张向阳的物理课》第一百零八期与第一百零九期别离在12月9日12时与12月11日12时开播,搜狐开创人、董事局主席兼CEO张向阳坐镇搜狐视频曲播间,先给网友们复习了伯努利定理以及对它的理解,然后引进粘滞系数不为零时不成压缩流体的纳维尔-斯托克斯方程,继而介绍起流体的剪切力,将其妥帖到了一般的应力张量上,并类比得到一般应力张量所对应的力密度公式,最初推导出纳维尔-斯托克斯方程。
复习伯努利定理 妥帖欧拉方程
在之前的曲播课程中,张向阳介绍了流体力学中的根本概念,并证明了伯努利定理。起首,假设流体是不成压缩的,而且流体处于稳恒活动的形态,也就是说
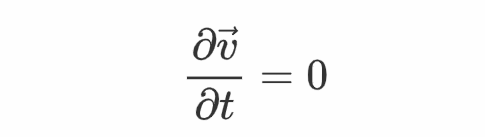
假设定义
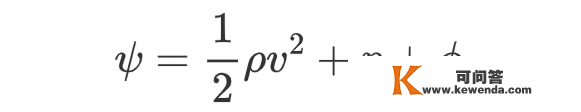
展开全文
此中ρ是流体密度,p是压强,Φg为单元体积的重力势。那么能够证明,当dr沿着流线标的目的时有
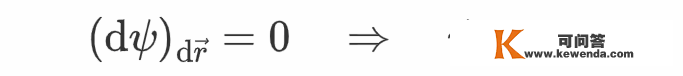
此中“ψ=常数”指的是它在整个流线上连结为常数。
在之前的曲播课程中,张向阳也讲到,抱负流体的“运动方程”为欧拉方程:
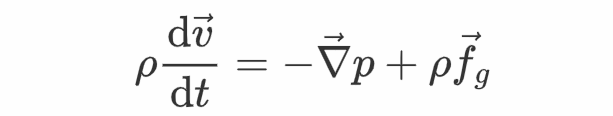
此中的加速度表达的是流体微元在流体前进时的加速度,f_g是重力体密度。一般来说,流体的速度散布不只依靠于时间,还依靠于空间位置。流体微元在活动的过程中,其速度等于速度场在那个微元所在位置处的值。因而,流体微元的加速度能够根据求导的链式法例写为
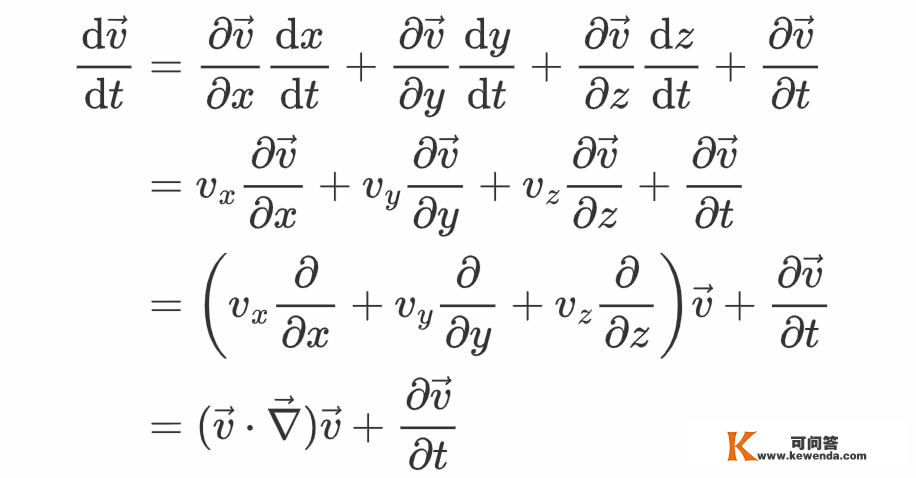
张向阳阐明说,最初一行的第一项能够理解为流体微元因位置改动而招致的速度改变所对应的加速度,第二项为流速场随时间改动而招致的加速度。将上式的成果代进欧拉方程能够得到
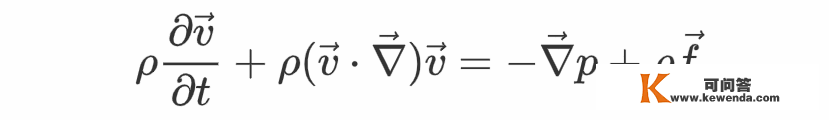
张向阳考虑了一个沿着径向逐步变窄然后又逐步恢复本来半径的管子,有不成压缩抱负流体在此中稳恒活动:
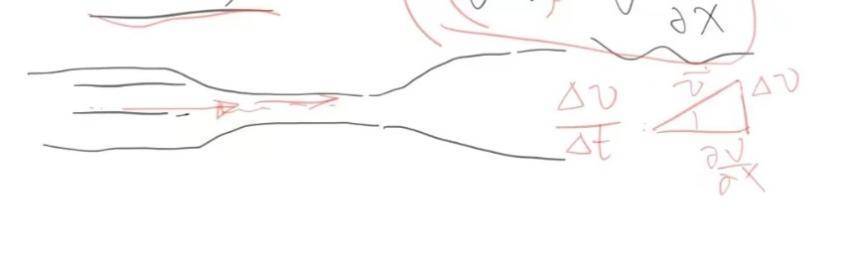
因为流体不成压缩,水管窄处的流体速度一定大于粗处的流体速度,根据伯努利定理,窄处的压强相对较小,粗处的压强相对较大,因而压强的负梯度从管粗的处所指向管细的处所,所以流体在进进细管时会被压强招致的力所加速,而流出细管时则会被减速,那正好与“细管位置的流体速度相对较大”相吻合。另一方面,因为那里是稳恒活动,速度场对时间的偏导数等于零,但因为速度在差别位置纷歧样,从加速度公式可知,流体微元的加速度其实不等于零,那一点与刚刚的压强阐发相吻合。
介绍完欧拉方程与伯努利定理的理解之后,张向阳转而起头介绍粘滞系数不为零的不成压缩流体。关于如许的流体,它在活动过程中会因为本身内部的摩擦而损耗能量。能够通过一个被称为粘滞系数的常数μ来表征那种流体的“内摩擦”效应的强弱。考虑了粘滞系数之后,欧拉方程将会变成
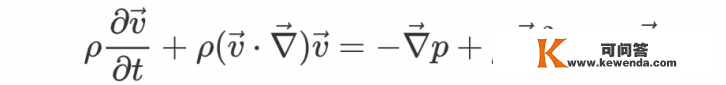
那个方程被称为纳维尔-斯托克斯方程,即Navier-Stokes equations,有时候简写为N-S方程。

(张向阳复习伯努利定理并介绍纳维尔-斯托克斯方程)
阐发应力张量 妥帖得到应力体密度
为了理解粘滞效应,需要从最简单的剪切运动起头说起。张向阳考虑了一个只沿着x标的目的运动的流体,其速度v跟着y坐标的增大而增大:

从微看角度来看,因为分子扩散,速度高的流体微元的分子会逐步向外扩散,速度低的流体微元的分子也会向外扩散,那就使得速度高的流体微元会领受来自速度低的区域的分子,从而那个微元的均匀速度会降低,而速度低的流体微元会领受来自速度高的区域的分子,于是那个微元的均匀速度会增大。那种动量的传递在宏看上可表示为粘滞力。粘滞力与压力一样,是一种感化在某个面上的力,因而能够定义一个与压强类似的量:单元面积的剪切力,被称为剪切应力,它的大小一般与速度场的改变率成反比:
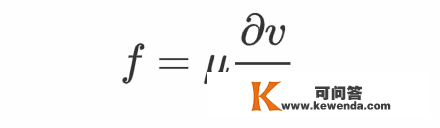
称心上式关系的流体被称为牛顿流体,非牛顿流体的剪切应力不反比于速度场的空间改变率。在上图中,假设取xz平面,法向指向y的正标的目的,那么f感化在那个面上,标的目的指向x轴正标的目的,它的意义就是xz平面上部的流体感化在xz平面下部的流体的力的面密度。假设取xz面的法向指向y的负标的目的,那么f的大小稳定,标的目的要酿成x轴负标的目的,f的意义则酿成了xz平面下部的流体感化在xz平面上部流体的力面密度。由此可见,剪切应力依靠于所拔取的面以及面的取向,那个性量与流体压强是一样的。
张向阳供给了一种理解上式的体例。假设一个高为Δy的矩形弹性体被掰成上图那样的平行四边形,此中斜边的倾角大小为Δθ,矩形顶部程度偏移量为Δx,那么类似于正向压缩的胡克定律,剪切的胡克定律为
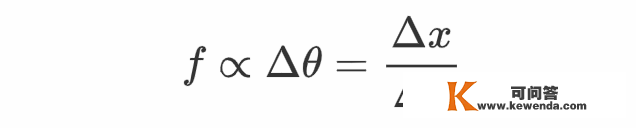
但是,流体与弹性体差别,流体在活动变形之后不会主动恢复外形,它的剪切应力来自于它的“继续形变”而非“单次形变”。张向阳提醒网友们,考虑一个悬挂着的球,一辆很长的火车从球边颠末,每个车窗都有人伸出手来朝统一个标的目的拍一下球,那么那个球的悬链就会在继续的拍击下连结一个固定的倾斜角度Δθ。假设球链长为Δy,球的程度偏移为Δx,火车速度为v,拍球间隔为Δt。因为每拍一次球其实就是停止一次动量传递,能够合理地认为在Δt时间内传递的动量反比于Δθ,于是有
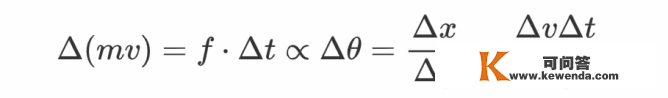
所以
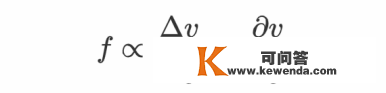
张向阳接着介绍说,一般地,描述应力需要用到应力张量,它能够写为一个三阶方阵的形式:

在流体内部取一个法向为x正标的目的的面积微元,那么流体感化在那个面积微元上的应力为
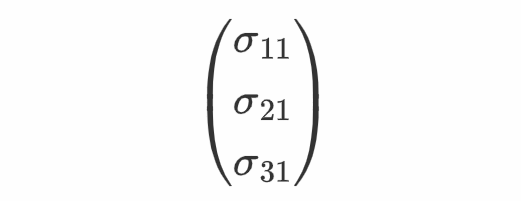
那就是应力张量第一列的物理意义。应力张量的第二、第三列也具有类似的意义,只不外所对应的面积微元的法向别离为y轴正标的目的与z轴正标的目的。有时应力张量的下标不利用数字而利用坐标符号,好比σ12能够写成σ_{xy}。
关于静行的流体或者抱负流体,它没有切应力,只要压强。压强是一种特殊的应力,标的目的与面积微元的法向相反,因而根据应力张量的物理意义可知,静流体以及抱负流体的应力张量形式为

或者,可借助狄拉克符号表达为
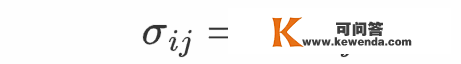
关于静行流体,取此中一个立方体体元,立方体各边都平行于坐标轴,边长别离为Δx、Δy、Δz,那么此体元遭到的来自四周流体的力的x重量为
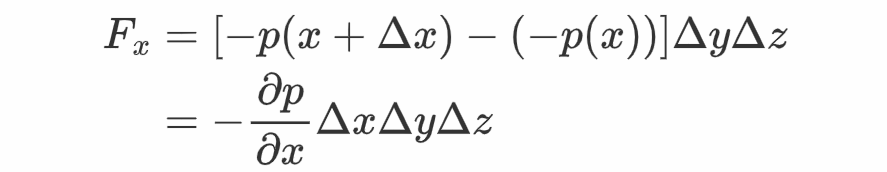
那个力对应的体密度为
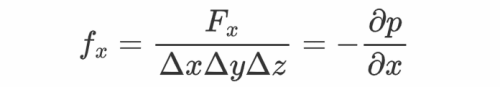
同理可得其他标的目的的力的体密度为
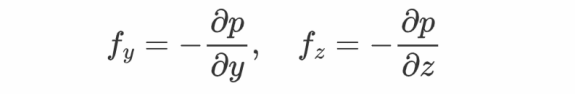
那些成果的矢量形式为
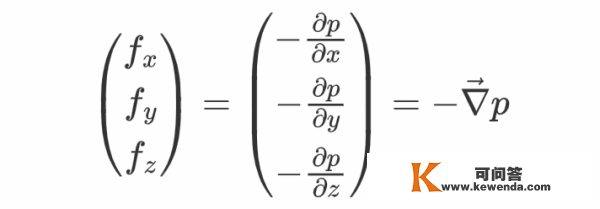
那个成果在之前的曲播课程中就已经被推导过了,不外它还能够借助应力张量而变形为
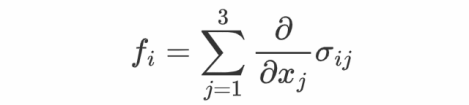
那个成果其实是普及成立的,能够借助应力张量的物理意义,通过取立方体微元的体例来证明。
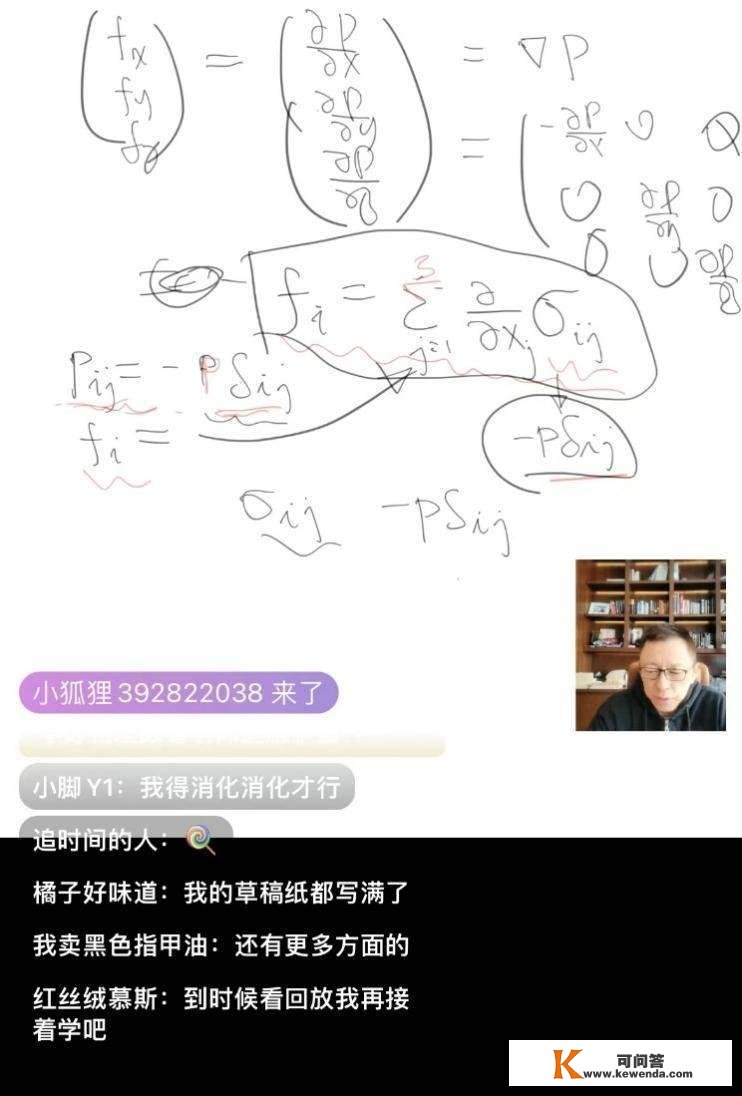
(张向阳介绍应力张量所招致的力体密度)
觅觅应力张量与速度场的关系 推导纳维尔-斯托克斯定理
前面讲到,静流体或者抱负流体的应力张量为

关于处于一般形态的流体,其应力张量的非对角元其实不为零,不外总能够写成如下形式:
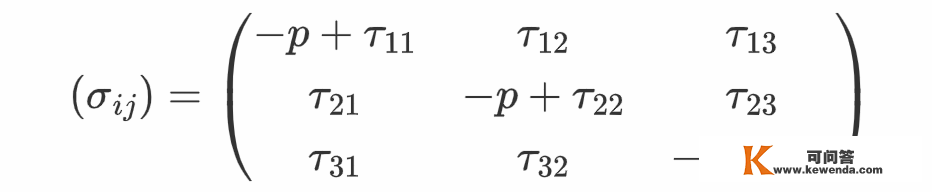
考虑前面介绍的流体做纯剪切运动时的情状:

根据牛顿流体的性量以及应力张量各重量的意义,可得
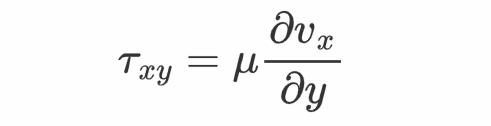
考虑此流体的一个平行于各个坐标轴的立方体元,边长别离为Δx、Δy、Δz。它的平行于xz平面的两个面,所遭到的剪切力刚好是相反的,因而那两个剪切力对此体元的力矩标的目的不异,两者之和为
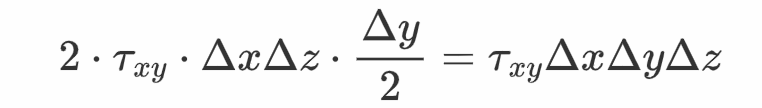
根据上述两个面的剪切力的标的目的可知,此力矩指向z轴负标的目的。
因为应力τ_{xy}在此体元上连结为常数,因而上述力矩是立体微元边长的三阶无限小量。而立体微元的动弹惯量是微元边长的五阶无限小量,因而在微元边长趋势于零的过程中,微元动弹惯量将比较矩减小得更快,那意味着此微元在足够小的时候会被那个力矩动弹得十分快,那是不成能的——除非有此外力矩能够与此力矩相平衡。来自外部的力大约感化在微元的中心,那几乎不奉献什么力矩。根据力的标的目的可推知,可以平衡此力矩的唯有ΔyΔz面上的应力y重量了。根据前面力矩的计算体例,能够得到ΔyΔz面上的应力y重量对应的力矩为
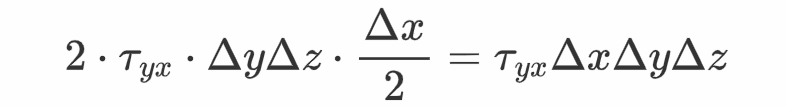
上式对应的力矩标的目的为z轴正标的目的。要想力矩可以抵消,一定有
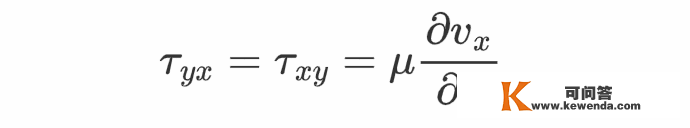
可见,v_x在y标的目的上的改变率也会对τ_{yx}有奉献。同样,v_y在x标的目的的改变率除了对τ_{yx}有奉献之外,还会对τ_{xy}有奉献。因而,在一般的速度场下,应有
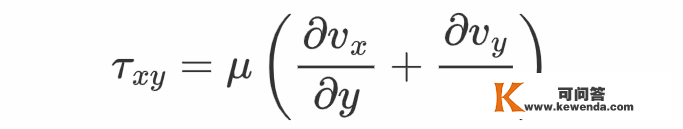
关于τ的其他非对角重量,有

需要重视的是,上述对τ_{xy}的阐发体例不适用于τ的对角重量。不外,能够根据τ的非对角元的形式通过扭转变更来得到τ的对角元形式。当τ的非对角元称心如上等式时,连系应力各向同性的要求,最末可得一般形式的应力张量形式,此中对角元会加上一些与速度散度成反比的项,考虑到流体不成压缩,速度场的散度为零,所以那些对角项与非对角项的形式一致。于是,τ各个重量的形式为

可见,τ的对角元纷歧定为零,速度场的不平均性会给正应力带来影响。好比,τ_{xx}为
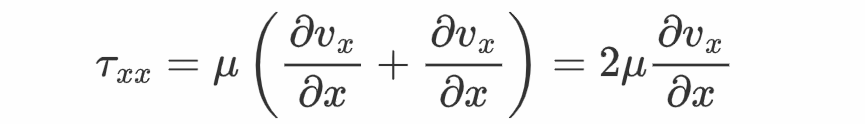
可见当v_x跟着x坐标增大而增大时,感化在法向为x正标的目的的面积微元上的正应力大小比压强p要小。
有了那些成果,就能够推导纳维尔-斯托克斯方程了。当有粘滞力存在时,原始的欧拉方程需要添加应力体密度那一项。根据前面的阐发,应力体密度的x重量为
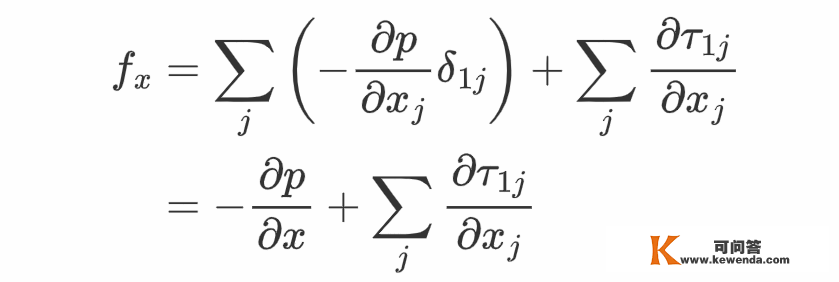
此中
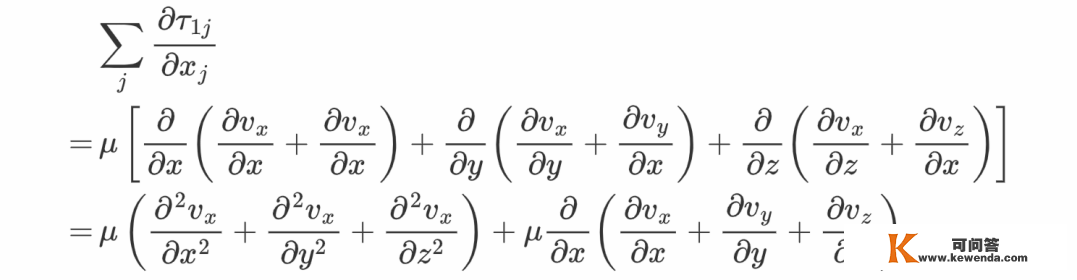
因为流体不成压缩,所以
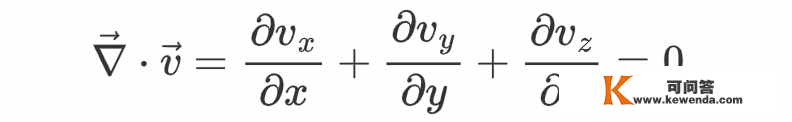
又因为
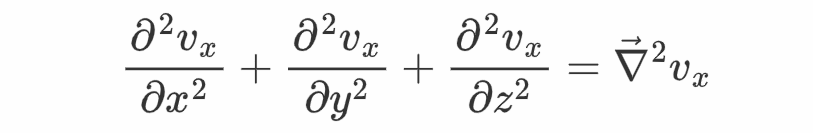
所以
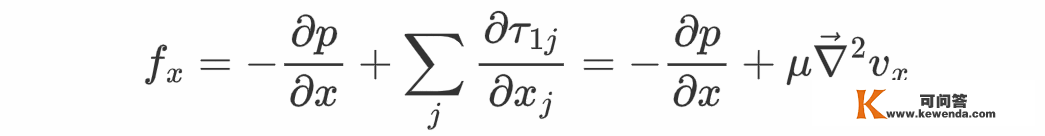
其他重量能够类似得到,最末有
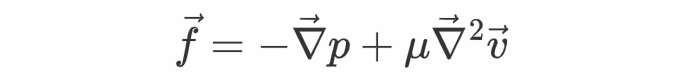
将其代进流体微元的牛顿第二定律中可得
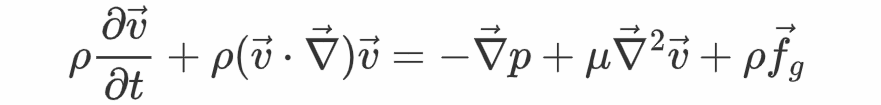
那就是前面介绍的纳维尔-斯托克斯方程,张向阳介绍说,它相当于流体力学中的“牛顿第二定律”。

(张向阳推导纳维尔-斯托克斯方程)
据领会,《张向阳的物理课》于每周周五、周日中午12时在搜狐视频曲播,网友能够在搜狐视频“存眷流”中搜刮“张向阳”,看看曲播及往期完全视频回放;存眷“张向阳的物理课”账号,查看课程中的“常识点”短视频。此外,还能够在搜狐新闻APP的“搜狐科技”账号上,阅览每期物理课程的详尽文章。
