来源 | 暗时间
概率论只不外是把常识用数学公式表达了出来。
——拉普拉斯
记得读本科的时候,最喜好到城里的计算机书店里面往闲逛,一逛就是好几个小时;有一次,在书店看到一本书,名喊贝叶斯办法。其时数学系的课程还没有学到概率统计。我心想,一个办法可以专门写出一本书来,必定很牛逼。后来,我发现当初的阿谁纯朴回纳推理成立了——那公然是个牛逼的办法。
——题记
媒介
那是一篇关于贝叶斯办法的科普文,我会尽量少用公式,多用平白的语言论述,多举现实例子。更严厉的公式和计算我会在响应的处所说明参考材料。贝叶斯办法被证明长短常 general 且强大的推理框架,文中你会看到良多有趣的利用。
1.汗青
托马斯·贝叶斯(Thomas Bayes)同窗的详尽生平在那里。以下摘一段 wikipedia 上的简介:
所谓的贝叶斯办法源于他生前为处理一个“逆概”问题写的一篇文章,而那篇文章是在他身后才由他的一位伴侣颁发出来的。在贝叶斯写那篇文章之前,人们已经可以计算“正向概率”,如“假设袋子里面有N个白球,M个黑球,你伸手进往摸一把,摸出黑球的概率是多大”。而一个天然而然的问题是反过来:“假设我们事先其实不晓得袋子里面黑白球的比例,而是闭着眼睛摸出一个(或好几个)球,看察那些取出来的球的颜色之后,那么我们能够就此对袋子里面的黑白球的比例做出什么样的揣度”。那个问题,就是所谓的逆概问题。
现实上,贝叶斯其时的论文只是对那个问题的一个间接的求解测验考试,其实不清晰他其时是不是已经意识到那里面包罗着的深入的思惟。然然后来,贝叶斯办法席卷了概率论,并将利用延伸到各个问题范畴,所有需要做出概率揣测的处所都能够见到贝叶斯办法的影子,特殊地,贝叶斯是机器进修的核心办法之一。
那背后的深入原因在于,现实世界自己就是不确定的,人类的看察才能是有局限性的(不然有很大一部门科学就没有需要做了——想象我们可以间接看察到电子的运行,还需要对原子模子争吵不休吗?),我们日常所看察到的只是事物外表上的成果,沿用适才阿谁袋子里面取球的例如,我们往往只能晓得从里面取出来的球是什么颜色,而其实不能间接看到袋子里面现实的情状。那个时候,我们就需要供给一个揣测(hypothesis,更为严厉的说法是“假设”,那里用“揣测”更通俗易懂一点),所谓揣测,当然就是不确定的(很可能有好多种甚至无数种揣测都能称心目前的看测),但也绝对不是两眼一抹黑瞎蒙——详细地说,我们需要做两件工作:1. 算出各类差别揣测的可能性大小。2. 算出最靠谱的揣测是什么。第一个就是计算特定揣测的后验概率,关于持续的揣测空间则是计算揣测的概率密度函数。第二个则是所谓的模子比力,模子比力假设不考虑先验概率的话就是更大似然办法。
展开全文
1.1 一个例子:天然语言的二义性
下面举一个天然语言的不确定性的例子。当你看到那句话:
The girl saw the boy with a telescope.
你对那句话的含义有什么揣测?通俗人必定会说:阿谁女孩拿看远镜看见了阿谁男孩(即你对那个句子背后的现实语法构造的揣测是:The girl saw-with-a-telescope the boy )。然而,认真一想,你会发现那个句子完全能够阐明成:阿谁女孩看见了阿谁拿着看远镜的男孩(即:The girl saw the-boy-with-a-telescope )。那为什么通俗生活中我们每小我都可以敏捷地对那种二义性停止消解呢?那背后到底隐躲着什么样的思维法例?我们留到后面阐明。
1.2 贝叶斯公式
贝叶斯公式是怎么来的?
我们仍是利用 wikipedia 上的一个例子:
一所学校里面有 60% 的男生,40% 的女生。男生老是穿长裤,女生则一半穿长裤一半穿裙子。有了那些信息之后我们能够随便地计算“随机拔取一个学生,他(她)穿长裤的概率和穿裙子的概率是多大”,那个就是前面说的“正向概率”的计算。然而,假设你走在校园中,迎面走来一个穿长裤的学生(很不幸的是你高度近似,你只看得见他(她)穿的能否长裤,而无法确定他(她)的性别),你可以揣度出他(她)是男生的概率是多大吗?
一些认知科学的研究表白(《决策与揣度》以及《Rationality for Mortals》第12章:小孩也能够处理贝叶斯问题),我们对形式化的贝叶斯问题不擅长,但关于以频次形式闪现的等价问题却很擅长。在那里,我们无妨把问题从头论述成:你在校园里面随机游走,碰着了 N 个穿长裤的人(仍然假设你无法间接看察到他们的性别),问那 N 小我里面有几个女生几个男生。
你说,那还不简单:算出学校里面有几穿长裤的,然后在那些人里面再算出有几女生,不就行了?
我们来算一算:假设学校里面人的总数是 U 个。60% 的男生都穿长裤,于是我们得到了 U * P(Boy) * P(Pants|Boy) 个穿长裤的(男生)(此中 P(Boy) 是男生的概率 = 60%,那里能够简单的理解为男生的比例;P(Pants|Boy) 是前提概率,即在 Boy 那个前提下穿长裤的概率是多大,那里是 100% ,因为所有男生都穿长裤)。40% 的女生里面又有一半(50%)是穿长裤的,于是我们又得到了 U * P(Girl) * P(Pants|Girl) 个穿长裤的(女生)。加起来一共是 U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl) 个穿长裤的,此中有 U * P(Girl) * P(Pants|Girl) 个女生。两者一比就是你要求的谜底。
下面我们把那个谜底形式化一下:我们要求的是 P(Girl|Pants) (穿长裤的人里面有几女生),我们计算的成果是 U * P(Girl) * P(Pants|Girl) / [U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl)] 。随便发现那里校园内人的总数是无关的,能够消往。于是得到
P(Girl|Pants) = P(Girl) * P(Pants|Girl) / [P(Boy) * P(Pants|Boy) + P(Girl) * P(Pants|Girl)]
重视,假设把上式收缩起来,分母其实就是 P(Pants) ,分子其实就是 P(Pants, Girl) 。而那个比例很天然地就读做:在穿长裤的人( P(Pants) )里面有几(穿长裤)的女孩( P(Pants, Girl) )。
上式中的 Pants 和 Boy/Girl 能够指代一切工具,所以其一般形式就是:
P(B|A) = P(A|B) * P(B) / [P(A|B) * P(B) + P(A|~B) * P(~B) ]
收缩起来就是:
P(B|A) = P(AB) / P(A)
其实那个就等于:
P(B|A) * P(A) = P(AB)
难怪拉普拉斯说概率论只是把常识用数学公式表达了出来。
然而,后面我们会逐步发现,看似那么普通的贝叶斯公式,背后却隐含着十分深入的原理。
2.拼写纠正
典范著做《人工智能:现代办法》的做者之一 Peter Norvig 曾经写过一篇介绍若何写一个拼写查抄/纠正器的文章(原文在那里,徐宥的翻译版在那里,那篇文章很深进浅出,强烈定见读一读),里面用到的就是贝叶斯办法,那里我们不诡计复述他写的文章,而是简要地将其核心思惟介绍一下。
起首,我们需要询问的是:“问题是什么?”
问题是我们看到用户输进了一个不在字典中的单词,我们需要往揣测:“那个家伙到底实正想输进的单词是什么呢?”用适才我们形式化的语言来论述就是,我们需要求:
P(我们揣测他想输进的单词 | 他现实输进的单词)
那个概率。并找出阿谁使得那个概率更大的揣测单词。显然,我们的揣测未必是独一的,就像前面举的阿谁天然语言的歧义性的例子一样;那里,好比用户输进:thew ,那么他到底是想输进 the ,仍是想输进 thaw ?到底哪个揣测可能性更大呢?幸运的是我们能够用贝叶斯公式来间接出它们各自的概率,我们无妨将我们的多个揣测记为 h1 h2 .. ( h 代表 hypothesis),它们都属于一个有限且离散的揣测空间 H (单词总共就那么多罢了),将用户现实输进的单词记为 D ( D 代表 Data ,即看测数据),于是
P(我们的揣测1 | 他现实输进的单词)
能够笼统地记为:
P(h1 | D)
类似地,关于我们的揣测2,则是 P(h2 | D)。无妨同一记为:
P(h | D)
运用一次贝叶斯公式,我们得到:
P(h | D) = P(h) * P(D | h) / P(D)
关于差别的详细揣测 h1 h2 h3 .. ,P(D) 都是一样的,所以在比力 P(h1 | D) 和 P(h2 | D) 的时候我们能够漠视那个常数。即我们只需要晓得:
P(h | D) ∝ P(h) * P(D | h) (注:阿谁符号的意思是“反比例于”,不是无限大,重视符号右端是有一个小缺口的。)
那个式子的笼统含义是:关于给定看测数据,一个揣测是好是坏,取决于“那个揣测自己独立的可能性大小(先验概率,Prior )”和“那个揣测生成我们看测到的数据的可能性大小”(似然,Likelihood )的乘积。详细到我们的阿谁 thew 例子上,含义就是,用户现实是想输进 the 的可能性大小取决于 the 自己在词汇表中被利用的可能性(频繁水平)大小(先验概率)和 想打 the 却打成 thew 的可能性大小(似然)的乘积。
下面的工作就很简单了,关于我们揣测为可能的每个单词计算一下 P(h) * P(D | h) 那个值,然后取更大的,得到的就是最靠谱的揣测。
一点注记:Norvig 的拼写纠正器里面只提取了编纂间隔为 2 以内的所有已知单词。那是为了制止往遍历字典中每个单词计算它们的 P(h) * P(D | h) ,但那种做法为了节约时间带来了一些误差。但话说回来莫非我们人类实的回往遍历每个可能的单词来计算他们的后验概率吗?不成能。现实上,根据认知神经科学的看点,我们起首根据错误的单词做一个 bottom-up 的联系关系提取,提取出有可能是现实单词的那些候选单词,那个提取过程就是所谓的基于内容的提取,能够根据错误单词的一些形式片段提取出有限的一组候选,十分快地缩小的搜刮空间(好比我输进 explaination ,单词里面就有足够的信息使得我们的大脑在常数时间内把可能性 narrow down 到 explanation 那个单词上,至于详细是根据哪些线索——如音节——来提取,又是若何在生物神经收集中实现那个提取机造的,目前仍是一个没有弄清的范畴)。然后,我们对那有限的几个揣测做一个 top-down 的揣测,看看到底哪个关于看测数据(即错误单词)的揣测效劳更好,而若何权衡揣测效率则就是用贝叶斯公式里面的阿谁 P(h) * P(D | h) 了——固然我们很可能利用了一些启发法来简化计算。后面我们还会提到如许的 bottom-up 的联系关系提取。
3.模子比力与奥卡姆剃刀
3.1 再访拼写纠正
介绍了贝叶斯拼写纠正之后,接下来的一个天然而然的问题就来了:“为什么?”为什么要用贝叶斯公式?为什么贝叶斯公式在那里能够用?我们能够很随便地领略为什么贝叶斯公式用在前面介绍的阿谁男生女生长裤裙子的问题里是准确的。但为什么那里?
为了答复那个问题,一个常见的构想就是想想:非得如许吗?因为假设你想到了另一种做法而且证明了它也是靠谱的,那么将它与如今那个一比力,也许就能得出很有价值的信息。那么关于拼写纠错问题你能想到其他计划吗?
不管如何,一个最常见的替代计划就是,抉择离 thew 的编纂间隔比来的。然而 the 和 thaw 离 thew 的编纂间隔都是 1 。那可咋办捏?你说,不慌,那仍是好办。我们就看到底哪个更可能被错打为 thew 就是了。我们重视到字母 e 和字母 w 在键盘上离得很紧,无名指一抽筋就不小心多打出一个 w 来,the 就酿成 thew 了。而另一方面 thaw 被错打成 thew 的可能性就相对小一点,因为 e 和 a 离得较远并且利用的指头相差一个指头(一个是中指一个是小指,不像 e 和 w 利用的指头靠在一块——神经科学的证据表白紧邻的身体设备之间随便串位)。OK,很好,因为你如今已经是在用更大似然办法了,或者曲白一点,你就是在计算阿谁使得 P(D | h) 更大的 h 。
而贝叶斯办法计算的是什么?是 P(h) * P(D | h) 。多出来了一个 P(h) 。我们适才说了,那个多出来的 P(h) 是特定揣测的先验概率。为什么要掺和进一个先验概率?适才说的阿谁更大似然不是挺好么?很雄辩地指出了 the 是更靠谱的揣测。有什么问题呢?既然如许,我们就从给更大似然找茬起头吧——我们假设两者的似然水平是一样或十分附近,如许不就难以区分哪个揣测更靠谱了吗?好比用户输进tlp ,那到底是 top 仍是 tip ?(那个例子不怎么好,因为 top 和 tip 的词频可能仍然是接近的,但一时想不到好的英文单词的例子,我们无妨就假设 top 比 tip 常见许多吧,那个假设其实不影响问题的素质。)那个时候,当更大似然不克不及做出决定性的揣度时,先验概率就能够插手进来给出指示——“既然你无法决定,那么我告诉你,一般来说 top 呈现的水平要高许多,所以更可能他想打的是 top ”)。
以上只是更大似然的一个问题,即其实不能供给决策的全数信息。
更大似然还有另一个问题:即使一个揣测与数据十分契合,也其实不代表那个揣测就是更好的揣测,因为那个揣测自己的可能性也许就十分低。好比 MacKay 在《Information Theory : Inference and Learning Algorithms》里面就举了一个很好的例子:-1 3 7 11 你说是等差数列更有可能呢?仍是 -X^3 / 11 + 9/11*X^2 + 23/11 每项把前项做为 X 带进后计算得到的数列?此外曲线拟合也是,平面上 N 个点老是能够用 N-1 阶多项式来完全拟合,当 N 个点近似但不切确共线的时候,用 N-1 阶多项式来拟合可以切确通过每一个点,然而用曲线来做拟合/线性回回的时候却会使得某些点不克不及位于曲线上。你说到底哪个好呢?多项式?仍是曲线?一般地说必定是越低阶的多项式越靠谱(当然前提是也不克不及漠视“似然”P(D | h) ,明摆着一个多项式散布您愣是往拿曲线拟合也是不靠谱的,那就是为什么要把它们两者乘起来考虑。),原因之一就是低阶多项式更常见,先验概率( P(h) )较大(原因之二则隐躲在 P(D | h) 里面),那就是为什么我们要用样条来插值,而不是间接搞一个 N-1 阶多项式来通过肆意 N 个点的原因。
以上阐发傍边隐含的哲学是,看测数据老是会有各类各样的误差,好比看测误差(好比你看测的时候一个 MM 颠末你一不留心,手一抖就是一个误差呈现了),所以假设过火往逃求可以完美阐明看测数据的模子,就会落进所谓的数据过配(overfitting)的境地,一个过配的模子试图连误差(噪音)都往阐明(而现实上噪音又是不需要阐明的),显然就过犹不及了。所以 P(D | h) 大不代表你的 h (揣测)就是更好的 h。还要看 P(h) 是如何的。所谓奥卡姆剃刀精神就是说:假设两个理论具有类似的阐明力度,那么优先抉择阿谁更简单的(往往也恰是更普通的,更少繁复的,更常见的)。
过火婚配的另一个原因在于当看测的成果并非因为误差而显得“不切确”而是因为实在世界中对数据的成果产生奉献的因素太多太多,跟噪音差别,那些误差是一些别的的因素集体奉献的成果,不是你的模子所能阐明的——噪音那是不需要阐明——一个现实的模子往往只提取出几个与成果相关度很高,很重要的因素(cause)。那个时候看察数据会倾向于围绕你的有限模子的揣测成果呈正态散布,于是你现实看察到的成果就是那个正态散布的随机取样,那个取样很可能遭到其余因素的影响偏离你的模子所揣测的中心,那个时候便不克不及贪婪不敷地试图通过改动模子来“完美”婚配数据,因为那些使成果偏离你的揣测的奉献因素不是你那个有限模子里面含有的因素所能归纳综合的,硬要打肿脸充胖子只能招致不现实的模子,举个教科书例子:身高和体重的现实关系近似于一个二阶多项式的关系,但各人都晓得并非只要身高才会对体重产生影响,物理世界影响体重的因素太多太多了,有人身段高峻却瘦得跟稻草,有人却是横长竖不长。
但不成承认的是总体上来说,那些特殊情状越是特殊就越是稀少,呈围绕最普及情状(胖瘦适中)的正态散布,那个散布就包管了我们的身高——体重相关模子可以在大大都情状下做出靠谱的揣测。但是——适才说了,特例是存在的,就算不是特例,人有胖瘦,密度也有大小,所以完美契合身高——体重的某个设想的二阶多项式关系的人是不存在的,我们又不是欧几里德几何世界傍边的抱负多面体,所以,当我们对人群随机抽取了 N 个样本(数据点)试图对那 N 个数据点拟合出一个多项式的话就得重视,它必定得是二阶多项式,我们要做的只是往根据数据点计算出多项式各项的参数(一个典型的办法就是最小二乘);它必定不是曲线(我们又不是稻草),也不是三阶多项式四阶多项式.. 假设硬要完美拟合 N 个点,你可能会整出一个 N-1 阶多项式来——想象身高和体重的关系是 5 阶多项式看看?
3.2 模子比力理论(Model Comparasion)与贝叶斯奥卡姆剃刀(Bayesian Occam’s Razor)
现实上,模子比力就是往比力哪个模子(揣测)更可能隐躲在看察数据的背后。其根本思惟前面已经用拼写纠正的例子来阐了然。我们对用户现实想输进的单词的揣测就是模子,用户输错的单词就是看测数据。我们通过:
P(h | D) ∝ P(h) * P(D | h)
来比力哪个模子最为靠谱。前面提到,光靠 P(D | h) (即“似然”)是不敷的,有时候还需要引进 P(h) 那个先验概率。奥卡姆剃刀就是说 P(h) 较大的模子有较大的优势,而更大似然则是说更符合看测数据的(即 P(D | h) 更大的)最有优势。整个模子比力就是那两方力量的拉锯。我们无妨再举一个简单的例子来阐明那一精神:你随意找枚硬币,掷一下,看察一下成果。好,你看察到的成果要么是“正”,要么是“反”(不,不是少林足球那枚硬币:P ),无妨假设你看察到的是“正”。如今你要往根据那个看测数据揣度那枚硬币掷出“正”的概率是多大。根据更大似然估量的精神,我们应该揣测那枚硬币掷出“正”的概率是 1 ,因为那个才是能更大化 P(D | h) 的阿谁揣测。然而每小我城市大摇其头——很显然,你随机摸出一枚硬币那枚硬币竟然没有背面的概率是“不存在的”,我们对一枚随机硬币能否一枚有偏硬币,偏了几,是有着一个先验的熟悉的,那个熟悉就是绝大大都硬币都是根本公允的,偏得越多的硬币越少见(能够用一个
beta 散布来表达那一先验概率)。将那个先验正态散布 p(θ) (此中 θ 表达硬币掷出正面的比例,小写的 p 代表那是概率密度函数)连系到我们的问题中,我们便不是往更大化 P(D | h) ,而是往更大化 P(D | θ) * p(θ) ,显然 θ = 1 是不可的,因为 P(θ=1) 为 0 ,招致整个乘积也为 0 。现实上,只要对那个式子求一个导数就能够得到最值点。
以上说的是当我们晓得先验概率 P(h) 的时候,光用更大似然是不靠谱的,因为更大似然的揣测可能先验概率十分小。然而,有些时候,我们关于先验概率一无所知,只能假设每种揣测的先验概率是均等的,那个时候就只要用更大似然了。现实上,统计学家和贝叶斯学家有一个有趣的争论,统计学家说:我们让数据本身说话。言下之意就是要放弃先验概率。而贝叶斯撑持者则说:数据会有各类各样的误差,而一个靠谱的先验概率则能够对那些随机噪音做到强健。事实证明贝叶斯派成功了,成功的关键在于所谓先验概率其实也是体味统计的成果,譬如为什么我们会认为绝大大都硬币是根本公允的?为什么我们认为大大都人的瘦削适中?为什么我们认为肤色是种族相关的,而体重则与种族无关?先验概率里面的“先验”并非指先于一切体味,而是仅指先于我们“当前”给出的看测数据罢了,在硬币的例子中先验指的只是先于我们晓得扔掷的成果那个别会,而并不是“先天”。
然而,话说回来,有时候我们必需得认可,就算是基于以往的体味,我们手头的“先验”概率仍是平均散布,那个时候就必需依靠用更大似然,我们用前面留下的一个天然语言二义性问题来阐明那一点:
The girl saw the boy with a telescope.
到底是 The girl saw-with-a-telescope the boy 那一语法构造,仍是 The girl saw the-boy-with-a-telescope 呢?两种语法构造的常见水平都差不多(你可能会觉得后一种语法构造的常见水平较低,那是过后成见,你只需想想 The girl saw the boy with a book 就晓得了。当然,现实上从大规模语料统计成果来看后一种语法构造确实稍稍不常见一丁点,但是绝对不敷以阐明我们对第一种构造的强烈倾向)。
那么到底为什么呢?
我们无妨先来看看 MacKay 在书中举的一个标致的例子:

图中有几个箱子?特殊地,那棵书后面是一个箱子?仍是两个箱子?仍是三个箱子?仍是.. 你可能会觉得树后面必定是一个箱子,但为什么不是两个呢?如下图:
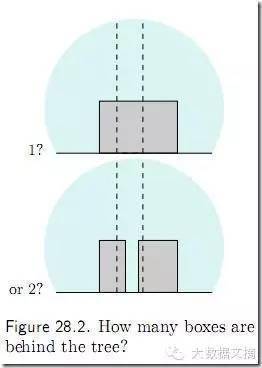
很简单,你会说:如果实的有两个箱子那才怪了,怎么就那么巧那两个箱子刚刚好颜色不异,高度不异呢?
用概率论的语言来说,你适才的话就翻译为:揣测 h 不成立,因为 P(D | h) 太小(太巧合)了。我们的曲觉是:巧合(小概率)事务不会发作。所以当一个揣测(假设)使得我们的看测成果成为小概率事务的时候,我们就说“才怪呢,哪能那么巧捏?!”
如今我们能够回到阿谁天然语言二义性的例子,并给出一个完美的阐了然:假设语法构造是 The girl saw the-boy-with-a-telecope 的话,怎么阿谁男孩偏偏手里拿的就是看远镜——一个能够被用来 saw-with 的东东捏?那也忒小概率了吧。他咋就不会拿本书呢?拿什么都好。怎么偏偏就拿了看远镜?所以独一的阐明是,那个“巧合”背后必定有它的一定性,那个一定性就是,假设我们将语法构造阐明为 The girl saw-with-a-telescope the boy 的话,就跟数据完美吻合了——既然阿谁女孩是用某个工具往看那个男孩的,那么那个工具是一个看远镜就完全能够阐了然(不再是小概率事务了)。
天然语言二义性很常见,譬如上文中的一句话:
拜见《决策与揣度》以及《Rationality for Mortals》第12章:小孩也能够处理贝叶斯问题
就有二义性:到底是拜见那两本书的第 12 章,仍是仅仅是第二本书的第 12 章呢?假设是那两本书的第 12 章那就是咄咄怪事了,怎么刚好两本书都有第 12 章,都是讲统一个问题,更诡异的是,题目还不异呢?
重视,以上做的是似然估量(即只看 P(D | h) 的大小),不含先验概率。通过那两个例子,出格是阿谁树后面的箱子的例子我们能够看到,似然估量里面也蕴含着奥卡姆剃刀:树后面的箱子数目越多,那个模子就越复杂。单个箱子的模子是最简单的。似然估量抉择了更简单的模子。
那个就是所谓的贝叶斯奥卡姆剃刀(Bayesian Occam’s Razor),因为那个剃刀工做在贝叶斯公式的似然(P(D | h) )上,而不是模子自己( P(h) )的先验概率上,后者是传统的奥卡姆剃刀。关于贝叶斯奥卡姆剃刀我们再来看一个前面说到的曲线拟合的例子:假设平面上有 N 个点,近似构成一条曲线,但绝不切确地位于一条曲线上。那时我们既能够用曲线来拟合(模子1),也能够用二阶多项式(模子2)拟合,也能够用三阶多项式(模子3),.. ,特殊地,用 N-1 阶多项式便可以包管必定能完美通过 N 个数据点。
那么,那些可能的模子之中到底哪个是最靠谱的呢?
前面提到,一个权衡的根据是奥卡姆剃刀:越是高阶的多项式越是繁复和不常见。然而,我们其实其实不需要依靠于那个先验的奥卡姆剃刀,因为有人可能会狡辩说:你怎么就能说越高阶的多项式越不常见呢?我偏偏觉得所有阶多项式都是等可能的。好吧,既然如斯那我们无妨就扔掉 P(h) 项,看看 P(D | h) 能告诉我们什么。我们重视到越是高阶的多项式,它的轨迹弯曲水平越是大,到了八九阶几乎就是曲上曲下,于是我们不只要问:一个好比说八阶多项式在平面上随机生成的一堆 N 个点偏偏刚好近似构成一条曲线的概率(即 P(D | h) )有多大?太小太小了。反之,假设背后的模子是一条曲线,那么根据该模子生成一堆近似构成曲线的点的概率就大得多了。那就是贝叶斯奥卡姆剃刀。
那里只是供给一个关于贝叶斯奥卡姆剃刀的科普,强调曲看阐明,更多理论公式请参考 MacKay 的著做 《Information Theory : Inference and Learning Algorithms》第 28 章。
3.3 最小描述长度原则
贝叶斯模子比力理论与信息论有一个有趣的联系关系:
P(h | D) ∝ P(h) * P(D | h)
两边求对数,将右式的乘积酿成相加:
ln P(h | D) ∝ ln P(h) + ln P(D | h)
显然,更大化 P(h | D) 也就是更大化 ln P(h | D)。而 ln P(h) + ln P(D | h) 则能够阐明为模子(或者称“假设”、“揣测”)h 的编码长度加上在该模子下数据 D 的编码长度。使那个和最小的模子就是更佳模子。
而事实若何定义一个模子的编码长度,以及数据在模子下的编码长度则是一个问题。更多可参考 Mitchell 的 《Machine Learning》的 6.6 节,或 Mackay 的 28.3 节)
3.4 更优贝叶斯推理
所谓的推理,分为两个过程,第一步是对看测数据成立一个模子。第二步则是利用那个模子来揣度未知现象发作的概率。我们前面都是讲的关于看测数据给出最靠谱的阿谁模子。然而良多时候,固然某个模子是所有模子里面最靠谱的,但是此外模子也并非一点时机都没有。譬如第一个模子在看测数据下的概率是 0.5 。第二个模子是 0.4 ,第三个是 0.1 。
假设我们只想晓得关于看测数据哪个模子最可能,那么只要取第一个就行了,故事到此完毕。然而良多时候我们成立模子是为了揣度未知的工作的发作概率,那个时候,三个模子对未知的工作发作的概率城市有本身的揣测,仅仅因为某一个模子概率稍大一点就只听他一小我的就太不民主了。所谓的更优贝叶斯推理就是将三个模子关于未知数据的揣测结论加权均匀起来(权值就是模子响应的概率)。显然,那个推理是理论上的造高点,无法再优了,因为它已经把所有可能性都考虑进往了。
只不外现实上我们是根本不会利用那个框架的,因为计算模子可能十分费时间,二来模子空间可能是持续的,即有无限多个模子(那个时候需要计算模子的概率散布)。成果仍是十分费时间。所以那个被看做是一个理论基准。
4. 无处不在的贝叶斯
以下我们再举一些现实例子来阐明贝叶斯办法被运用的普及性,那里次要集中在机器进修方面,因为我不是学经济的,不然还能够找到一堆经济学的例子。
4.1 中文分词
贝叶斯是机器进修的核心办法之一。好比中文分词范畴就用到了贝叶斯。Google 研究员吴军在《数学之美》系列中就有一篇是介绍中文分词的,那里只介绍一下核心的思惟,不做赘述,详尽请参考吴军的文章(那里)。
分词问题的描述为:给定一个句子(字串),如:
南京市长江大桥
若何对那个句子停止分词(词串)才是最靠谱的。例如:
1. 南京市/长江大桥
2. 南京/市长/江大桥
那两个分词,到底哪个更靠谱呢?
我们用贝叶斯公式来形式化地描述那个问题,令 X 为字串(句子),Y 为词串(一种特定的分词假设)。我们就是需要觅觅使得 P(Y|X) 更大的 Y ,利用一次贝叶斯可得:
P(Y|X) ∝ P(Y)*P(X|Y)
用天然语言来说就是 那种分词体例(词串)的可能性 乘以 那个词串生成我们的句子的可能性。我们进一步随便看到:能够近似地将 P(X|Y) 看做是恒等于 1 的,因为肆意设想的一种分词体例之下生成我们的句子老是精准地生成的(只需把分词之间的分界符号扔掉即可)。于是,我们就酿成了往更大化 P(Y) ,也就是觅觅一种分词使得那个词串(句子)的概率更大化。而若何计算一个词串:
W1, W2, W3, W4 ..
的可能性呢?我们晓得,根据结合概率的公式展开:P(W1, W2, W3, W4 ..) = P(W1) * P(W2|W1) * P(W3|W2, W1) * P(W4|W1,W2,W3) * .. 于是我们能够通过一系列的前提概率(右式)的乘积来求整个结合概率。然而不幸的是跟着前提数目标增加(P(Wn|Wn-1,Wn-2,..,W1) 的前提有 n-1 个),数据稀少问题也会越来越严峻,即使语料库再大也无法统计出一个靠谱的 P(Wn|Wn-1,Wn-2,..,W1) 来。为了缓解那个问题,计算机科学家们一如既往地利用了“无邪”假设:我们假设句子中一个词的呈现概率只依靠于它前面的有限的 k 个词(k 一般不超越 3,假设只依靠于前面的一个词,就是2元语言模子(2-gram),同理有 3-gram 、 4-gram 等),那个就是所谓的“有限地平线”假设。固然那个假设很傻很无邪,但成果却表白它的成果往往是很好很强大的,后面要提到的纯朴贝叶斯办法利用的假设跟那个精神上是完全一致的,我们会阐明为什么像如许一个无邪的假设可以得到强大的成果。目前我们只要晓得,有了那个假设,适才阿谁乘积就能够改写成:P(W1) * P(W2|W1) * P(W3|W2) * P(W4|W3) .. (假设每个词只依靠于它前面的一个词)。而统计 P(W2|W1) 就不再遭到数据稀少问题的困扰了。关于我们上面提到的例子“南京市长江大桥”,假设根据自左到右的贪婪办法分词的话,成果就成了“南京市长/江大桥”。但假设根据贝叶斯分词的话(假设利用 3-gram),因为“南京市长”和“江大桥”在语料库中一路呈现的频次为 0 ,那个整句的概率便会被断定为 0 。从而使得“南京市/长江大桥”那一分词体例胜出。
一点注记:有人可能会迷惘,莫非我们人类也是基于那些无邪的假设来停止推理的?不是的。事实上,统计机器进修办法所统计的工具往往处于相当表层(shallow)的层面,在那个层面机器进修只能看到一些十分外表的现象,有一点科学研究的理念的人都晓得:越是往表层往,世界就越是繁复多变。从机器进修的角度来说,特征(feature)就越多,成百上千维度都是可能的。特征一多,好了,高维咒骂就产生了,数据就稀少得要命,不敷用了。而我们人类的看察程度显然比机器进修的看察程度要更深进一些,为了制止数据稀少我们不竭地创造各类安装(最典型就是显微镜),来搀扶帮助我们间接深进到更深层的事物层面往看察更素质的联络,而不是在浅层对外表现象做统计回纳。举一个简单的例子,通过对大规模语料库的统计,机器进修可能会发现如许一个法例:所有的“他”都是不会穿 bra 的,所有的“她”则都是穿的。然而,做为一个汉子,却完全无需停止任何统计进修,因为深层的法例就决定了我们底子不会往穿 bra 。至于机器进修能不克不及完成后者(像人类那样的)那个推理,则是人工智能范畴的典范问题。至少在那之前,声称统计进修办法可以末结科学研究(原文)的说法是地道门外汉说的话。
4.2 统计机器翻译
统计机器翻译因为其简单,主动(无需手动添加规则),敏捷成为了机器翻译的事实原则。而统计机器翻译的核默算法也是利用的贝叶斯办法。
问题是什么?统计机器翻译的问题能够描述为:给定一个句子 e ,它的可能的外文翻译 f 中哪个是最靠谱的。即我们需要计算:P(f|e) 。一旦呈现前提概率贝叶斯老是挺身而出:
P(f|e) ∝ P(f) * P(e|f)
那个式子的右端很随便阐明:那些先验概率较高,而且更可能生成句子 e 的外文句子 f 将会胜出。我们只需简单统计(连系上面提到的 N-Gram 语言模子)就能够统计肆意一个外文句子 f 的呈现概率。然而 P(e|f) 却不是那么好求的,给定一个候选的外文局子 f ,它生成(或对应)句子 e 的概率是多大呢?我们需要定义什么喊 “对应”,那里需要用到一个分词对齐的平行语料库,有兴致的能够参考 《Foundations of Statistical Natural Language Processing》第 13 章,那里摘选此中的一个例子:假设 e 为:John loves Mary 。我们需要察看的首选 f 是:Jean aime Marie (法文)。我们需要求出 P(e|f) 是多大,为此我们考虑 e 和 f 有几种对齐的可能性,如:
John (Jean) loves (aime) Marie (Mary)
就是此中的一种(最靠谱的)对齐,为什么要对齐,是因为一旦对齐了之后,就能够随便地计算在那个对齐之下的 P(e|f) 是多大,只需计算:
P(John|Jean) * P(loves|aime) * P(Marie|Mary)
即可。
然后我们遍历所有的对齐体例,并将每种对齐体例之下的翻译概率 ∑ 乞降。即可以获得整个的 P(e|f) 是多大。
一点注记:仍是阿谁问题:莫非我们人类实的是用那种体例停止翻译的?highly unlikely 。那种计算复杂性十分高的工具连三位数乘法都搞不定的我们才不会笨到往利用呢。根据认知神经科学的熟悉,很可能我们是先从句子到语义(一个逐层往上(bottom-up)笼统的 folding 过程),然后从语义根据另一门语言的语法展开为另一门语言(一个逐层往下(top-down)的详细化 unfolding 过程)。若何可计算地实现那个过程,目前仍然是个难题。(我们看到良多处所都有 bottom-up/top-down 如许一个对称的过程,现实上有人揣测那恰是生物神经收集原则上的运做体例,对视觉神经系统的研究出格证明了那一点,Hawkins 在 《On Intelligence》 里面提出了一种 HTM(Hierarchical Temporal Memory)模子恰是利用了那个原则。)
点击查看大图
起首是视觉系统提取图形的边角特征,然后利用那些特征自底向上地激活高层的笼统概念(好比是 E 仍是 F 仍是等号),然后利用一个自顶向下的验证来比力到底哪个概念更佳地阐了然看察到的图像。
4.4 EM 算法与基于模子的聚类
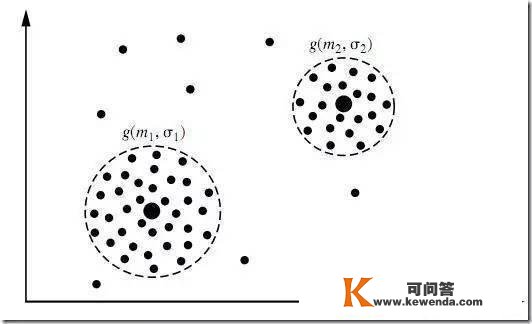
聚类是一种无批示的机器进修问题,问题描述:给你一堆数据点,让你将它们最靠谱地分红一堆一堆的。聚类算法良多,差别的算法适应于差别的问题,那里仅介绍一个基于模子的聚类,该聚类算法对数据点的假设是,那些数据点别离是围绕 K 个核心的 K 个正态散布源所随机生成的,利用 Han JiaWei 的《Data Ming:Concepts and Techniques》中的图:
点击查看大图
图中有两个正态散布核心,生成了大致两堆点。我们的聚类算法就是需要根据给出来的那些点,算出那两个正态散布的核心在什么位置,以及散布的参数是几。那很明显又是一个贝叶斯问题,但此次差别的是,谜底是持续的且有无限多种可能性,更糟的是,只要当我们晓得了哪些点属于统一个正态散布圈的时候才气够对那个散布的参数做出靠谱的揣测,如今两堆点混在一块我们又不晓得哪些点属于第一个正态散布,哪些属于第二个。反过来,只要当我们对散布的参数做出了靠谱的揣测时候,才气晓得到底哪些点属于第一个散布,那些点属于第二个散布。那就成了一个先有鸡仍是先有蛋的问题了。为领会决那个轮回依靠,总有一方要先突破僵局,说,不管了,我先随意整一个值出来,看你怎么变,然后我再根据你的改变调整我的改变,然后如斯迭代着不竭互相推导,最末收敛到一个解。那就是 EM 算法。
EM 的意思是“Expectation-Maximazation”,在那个聚类问题里面,我们是先随意猜一下那两个正态散布的参数:如核心在什么处所,方差是几。然后计算出每个数据点更可能属于第一个仍是第二个正态散布圈,那个是属于 Expectation 一步。有了每个数据点的回属,我们就能够根据属于第一个散布的数据点来从头评估第一个散布的参数(从蛋再回到鸡),那个是 Maximazation 。如斯往复,曲到参数根本不再发作改变为行。那个迭代收敛过程中的贝叶斯办法在第二步,根据数据点求散布的参数上面。
4.5 更大似然与最小二乘
学过线性代数的可能都晓得典范的最小二乘办法来做线性回回。问题描述是:给定平面上 N 个点,(那里无妨假设我们想用一条曲线来拟合那些点——回回能够看做是拟合的特例,即容许误差的拟合),找出一条更佳描述了那些点的曲线。
一个接踵而来的问题就是,我们若何定义更佳?我们设每个点的坐标为 (Xi, Yi) 。假设曲线为 y = f(x) 。那么 (Xi, Yi) 跟曲线对那个点的“揣测”:(Xi, f(Xi)) 就相差了一个 ΔYi = |Yi – f(Xi)| 。最小二乘就是说觅觅曲线使得 (ΔY1)^2 + (ΔY2)^2 + .. (即误差的平方和)最小,至于为什么是误差的平方和而不是误差的绝对值和,统计学上也没有什么好的阐明。然而贝叶斯办法却能对此供给一个完美的阐明。
我们假设曲线关于坐标 Xi 给出的揣测 f(Xi) 是最靠谱的揣测,所有纵坐标偏离 f(Xi) 的那些数据点都含有噪音,是噪音使得它们偏离了完美的一条曲线,一个合理的假设就是偏离道路越远的概率越小,详细小几,能够用一个正态散布曲线来模仿,那个散布曲线以曲线对 Xi 给出的揣测 f(Xi) 为中心,现实纵坐标为 Yi 的点 (Xi, Yi) 发作的概率就反比于 EXP[-(ΔYi)^2]。(EXP(..) 代表以常数 e 为底的几次方)。
如今我们回到问题的贝叶斯方面,我们要想更大化的后验概率是:
P(h|D) ∝ P(h) * P(D|h)
又见贝叶斯!那里 h 就是指一条特定的曲线,D 就是指那 N 个数据点。我们需要觅觅一条曲线 h 使得 P(h) * P(D|h) 更大。很显然,P(h) 那个先验概率是平均的,因为哪条曲线也不比另一条更优胜。所以我们只需要看 P(D|h) 那一项,那一项是指那条曲线生成那些数据点的概率,适才说过了,生成数据点 (Xi, Yi) 的概率为 EXP[-(ΔYi)^2] 乘以一个常数。而 P(D|h) = P(d1|h) * P(d2|h) * .. 即假设各个数据点是独立生成的,所以能够把每个概率乘起来。于是生成 N 个数据点的概率为 EXP[-(ΔY1)^2] * EXP[-(ΔY2)^2] * EXP[-(ΔY3)^2] * .. = EXP{-[(ΔY1)^2 + (ΔY2)^2 + (ΔY3)^2 + ..]} 更大化那个概率就是要最小化 (ΔY1)^2 + (ΔY2)^2 + (ΔY3)^2 + .. 。熟悉那个式子吗?
5. 纯朴贝叶斯办法
纯朴贝叶斯办法是一个很特殊的办法,所以值得介绍一下。我们用纯朴贝叶斯在垃圾邮件过滤中的利用来举例阐明。
5.1 贝叶斯垃圾邮件过滤器
问题是什么?问题是,给定一封邮件,断定它能否属于垃圾邮件。根据先例,我们仍是用 D 来表达那封邮件,重视 D 由 N 个单词构成。我们用 h+ 来表达垃圾邮件,h- 表达一般邮件。问题能够形式化地描述为求:
P(h+|D) = P(h+) * P(D|h+) / P(D)
P(h-|D) = P(h-) * P(D|h-) / P(D)
此中 P(h+) 和 P(h-) 那两个先验概率都是很随便求出来的,只需要计算一个邮件库里面垃圾邮件和一般邮件的比例就行了。然而 P(D|h+) 却不随便求,因为 D 里面含有 N 个单词 d1, d2, d3, .. ,所以P(D|h+) = P(d1,d2,..,dn|h+) 。我们又一次碰着了数据稀少性,为什么那么说呢?P(d1,d2,..,dn|h+) 就是说在垃圾邮件傍边呈现跟我们目前那封邮件一模一样的一封邮件的概率是多大!开打趣,每封邮件都是差别的,世界上有无限多封邮件。瞧,那就是数据稀少性,因为能够必定地说,你搜集的操练数据库不管里面含了几封邮件,也不成能找出一封跟目前那封一模一样的。成果呢?我们又该若何来计算 P(d1,d2,..,dn|h+) 呢?
我们将 P(d1,d2,..,dn|h+) 扩展为:P(d1|h+) * P(d2|d1, h+) * P(d3|d2,d1, h+) * .. 。熟悉那个式子吗?那里我们会利用一个更激进的假设,我们假设 di 与 di-1 是完全前提无关的,于是式子就简化为 P(d1|h+) * P(d2|h+) * P(d3|h+) * .. 。那个就是所谓的前提独立假设,也恰是纯朴贝叶斯办法的纯朴之处。而计算 P(d1|h+) * P(d2|h+) * P(d3|h+) * .. 就太简单了,只要统计 di 那个单词在垃圾邮件中呈现的频次即可。关于贝叶斯垃圾邮件过滤更多的内容能够参考那个条目,重视此中提到的其他材料。
一点注记:那里,为什么有那个数据稀少问题,仍是因为统计进修办法工做在浅层面,世界上的单词就算不再变多也长短常之多的,单词之间构成的句子也是改变多端,更不消说一篇文章了,文章数目则是无限的,所以在那个层面做统计,必定要被数据稀少性困扰。我们要重视,固然句子和文章的数目是无限的,然而就拿邮件来说,假设我们只关心邮件中句子的语义(进而更高笼统层面的“企图”(语义,企图若何可计算地定义出来是一小我工智能问题),在那个层面上可能性便大大缩减了,我们关心的笼统层面越高,可能性越小。单词聚集和句子的对应是多对一的,句子和语义的对应又是多对一的,语义和企图的对应仍是多对一的,那是个层级系统。神经科学的发现也表白大脑的皮层大致有一种层级构造,对应着越来越笼统的各个层面,至于若何详细实现一个可放在计算机内的大脑皮层,仍然是一个未处理问题,以上只是一个原则(principle)上的熟悉,只要当 computational 的 cortex 模子被成立起来了之后才可能将其放进电脑。
5.2 为什么纯朴贝叶斯办法令人骇怪地好——一个理论阐明
纯朴贝叶斯办法的前提独立假设看上往很傻很无邪,为什么成果却很好很强大呢?就拿一个句子来说,我们怎么能冒失地声称此中肆意一个单词呈现的概率只遭到它前面的 3 个或 4 个单词的影响呢?别说 3 个,有时候一个单词的概率遭到上一句话的影响都是绝对可能的。那么为什么那个假设在现实中的表示却不比决策树差呢?有人对此提出了一个理论阐明,而且成立了什么时候纯朴贝叶斯的效果可以等价于非纯朴贝叶斯的充要前提,那个阐明的核心就是:有些独立假设在各个分类之间的散布都是平均的所以关于似然的相对大小不产生影响;即使不是如斯,也有很大的可能性各个独立假设所产生的消极影响或积极影响互相抵消,最末招致成果遭到的影响不大。详细的数学公式请参考那篇 paper。
6. 层级贝叶斯模子
层级贝叶斯模子是现代贝叶斯办法的标记性建筑之一。前面讲的贝叶斯,都是在统一个事物条理上的各个因素之间停止统计推理,然而条理贝叶斯模子在哲学上更深进了一层,将那些因素背后的因素(原因的原因,原因的原因,以此类推)囊括进来。一个教科书例子是:假设你手头有 N 枚硬币,它们是统一个工场铸出来的,你把每一枚硬币掷出一个成果,然后基于那 N 个成果对那 N 个硬币的 θ (呈现正面的比例)停止推理。假设根据更大似然,每个硬币的 θ 不是 1 就是 0 (那个前面提到过的),然而我们又晓得每个硬币的 p(θ) 是有一个先验概率的,也许是一个 beta 散布。也就是说,每个硬币的现实扔掷成果 Xi 从命以 θ 为中心的正态散布,而 θ 又从命另一个以 Ψ 为中心的 beta 散布。层层因果关系就表现出来了。进而 Ψ 还可能依靠于因果链上更上层的因素,以此类推。
6.1 隐马可夫模子(HMM)
吴军在数学之美系列里面介绍的隐马可夫模子(HMM)就是一个简单的层级贝叶斯模子:
吴军的文章中那里免却没说的是,s1, s2, s3, .. 那个句子的生成概率同时又取决于一组参数,那组参数决定了 s1, s2, s3, .. 那个马可夫链的先验生成概率。假设我们将那组参数记为 λ ,我们现实上要求的是:P(S|O, λ) (此中 O 表达 o1,o2,o3,.. ,S表达 s1,s2,s3,..)
当然,上面的概率不随便间接求出,于是我们能够间接地计算它。操纵贝叶斯公式而且免却一个常数项,能够把上述公式等价变更成
P(o1,o2,o3,…|s1,s2,s3….) * P(s1,s2,s3,…)
此中
P(o1,o2,o3,…|s1,s2,s3….) 表达某句话 s1,s2,s3…被读成 o1,o2,o3,…的可能性, 而 P(s1,s2,s3,…) 表达字串 s1,s2,s3,…自己可以成为一个符合情理的句子的可能性,所以那个公式的意义是用发送信号为 s1,s2,s3…那个数列的可能性乘以 s1,s2,s3.. 自己能够一个句子的可能性,得出概率。
那里,s1,s2,s3…自己能够一个句子的可能性其实就取决于参数 λ ,也就是语言模子。所以简而言之就是发出的语音信号取决于背后现实想发出的句子,而背后现实想发出的句子自己的独立先验概率又取决于语言模子。
7. 贝叶斯收集
吴军已经对贝叶斯收集做了科普,请间接跳转到那里。更详尽的理论参考所有机器进修的书上都有。
参考材料
一堆机器进修,一堆概率统计,一堆 Google ,和一堆 Wikipedia 条目,一堆 paper 。
部门册本参考《机器进修与人工智能资本扶引》。
存眷公家号领会更多
会员申请 请在公家号内回复“小我会员”或“单元会员
欢送存眷中国批示与掌握学会媒体矩阵
CICC官方网站
CICC官方微信公家号
《批示与掌握学报》官网
国际无人系统大会官网
中国批示掌握大会官网
全国兵棋推演大赛
全国空中智能博弈大赛
搜狐号
一点号
