单载波的相关QAM信号中,本振激光与信号激光的频次差的允许范畴是几?
在单载波的相关光信号传输中,我们用一个本振(Local Oscillator)激光来将高频的载波光信号搬移到基频附近。凡是本振激光与信号激光的频次差别。若是频次不异的话,则不需要在数字信号处置中停止差频移除那一模块。当然,同频激光做本振,会给领受高频PD之后的跨阻放大器带来小小的问题。没有频差的信号被领受的时候,因为QAM信号自己是方形的,当其跟着激光的相位噪声迟缓扭转的时候,跨阻放大器的每个频道看到的是慢变的功率,而不是因为有频差而快速扭转的均匀后的功率,所以需要跨阻放大器及时调整其增益而跟上激光的相位噪声的变革。
若是本振激光与信号激光的频次差别,那么凡是允许几的频次不同呢?我们晓得当频次差为
Δf 时,相邻两个symbol之间的相位差是 Δϕ=2πΔfT_s 。但是因为QAM的信号每个symbol又有本身的相位,而且还有激光的相位噪声附加的一个能够用维纳过程做为模子的相位。如许一来增加了确定其由频次差带来的相位的难度。其实早在上个世纪,无线通信范畴就已经有探测频次差的处理计划。让我们以最简单的QPSK做为一个例子来切磋。
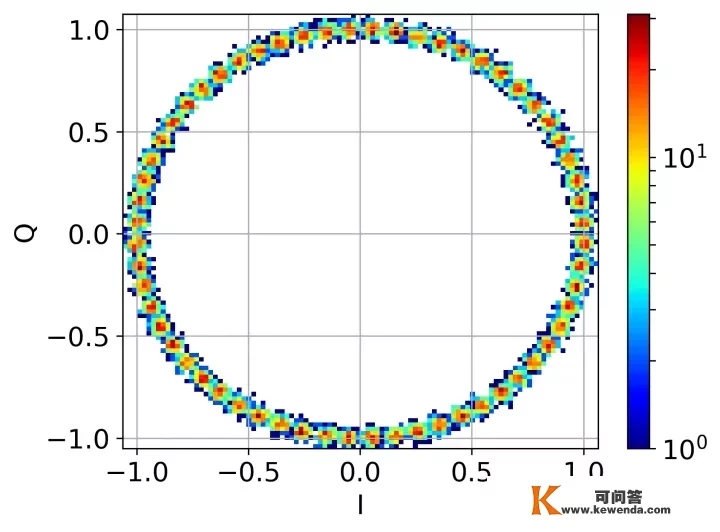
在做完equalization之后的QPSK信号是一个环,下图仿实了一个30 dB symbol信噪比的QPSK。在有normalization的情况下,其模值为1,而且为1个采样点对应一个symbol。接下来的操做就是要把如许一个模值为1的环复原回一般的QPSK星座图。

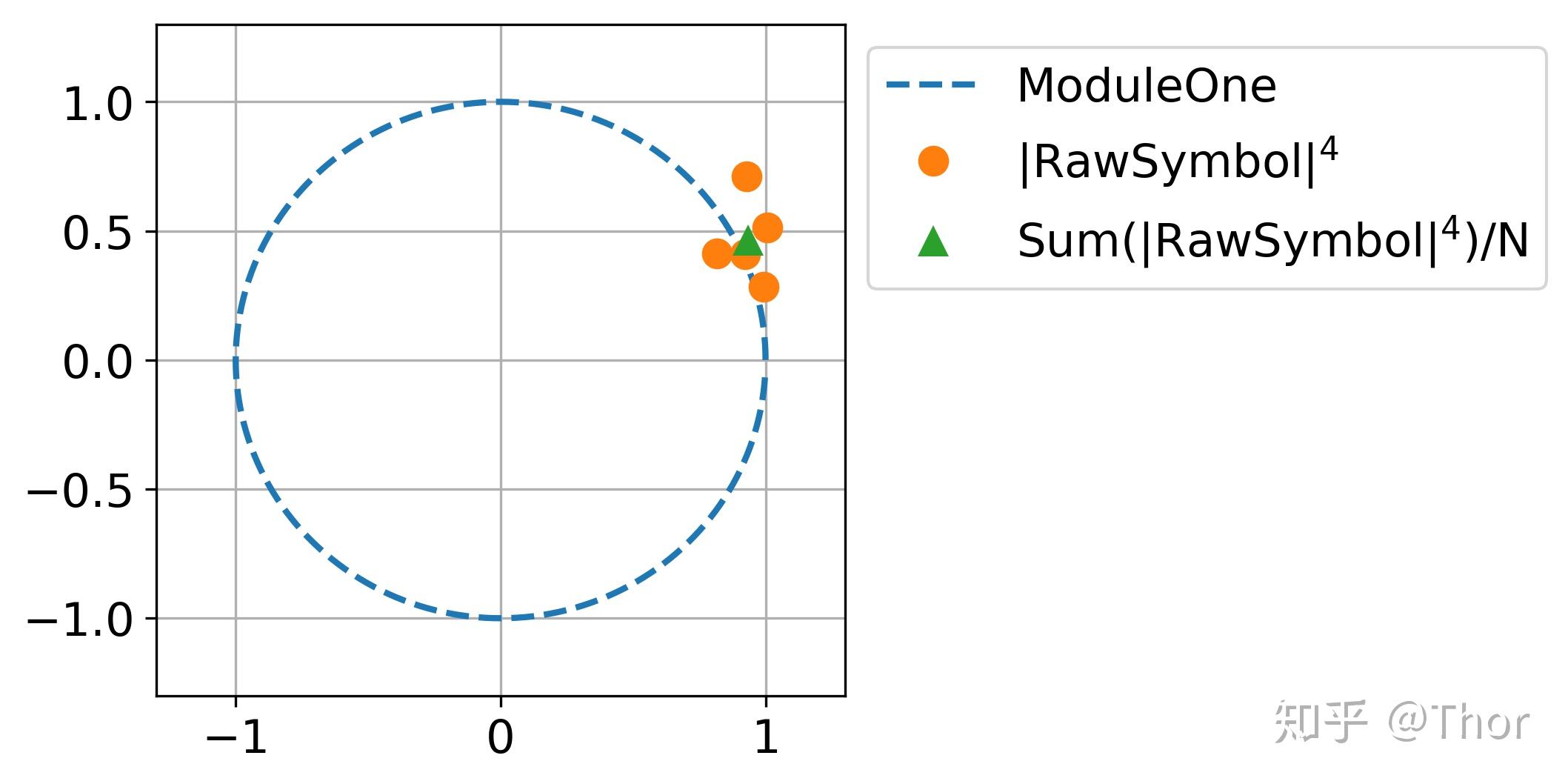
上图所示为一种十分遍及的检测差频的算法[1]。让我们来看看每一步都发作了什么。图示的左侧,每一个symbol和上一个symbol的共轭相乘,乘积之后的值包罗了相邻两个symbol之间的相位差,为了去除QPSK所加在symbol上的调造,我们把乘积值做四次方,相当于把幅角乘4, 剩余的相位差就是去除QPSK调造之后的相位差。取前后几个值做均匀去除信道的高斯噪声和激光的相位噪声。那个值会十分接近 4*2πΔfT_s 。
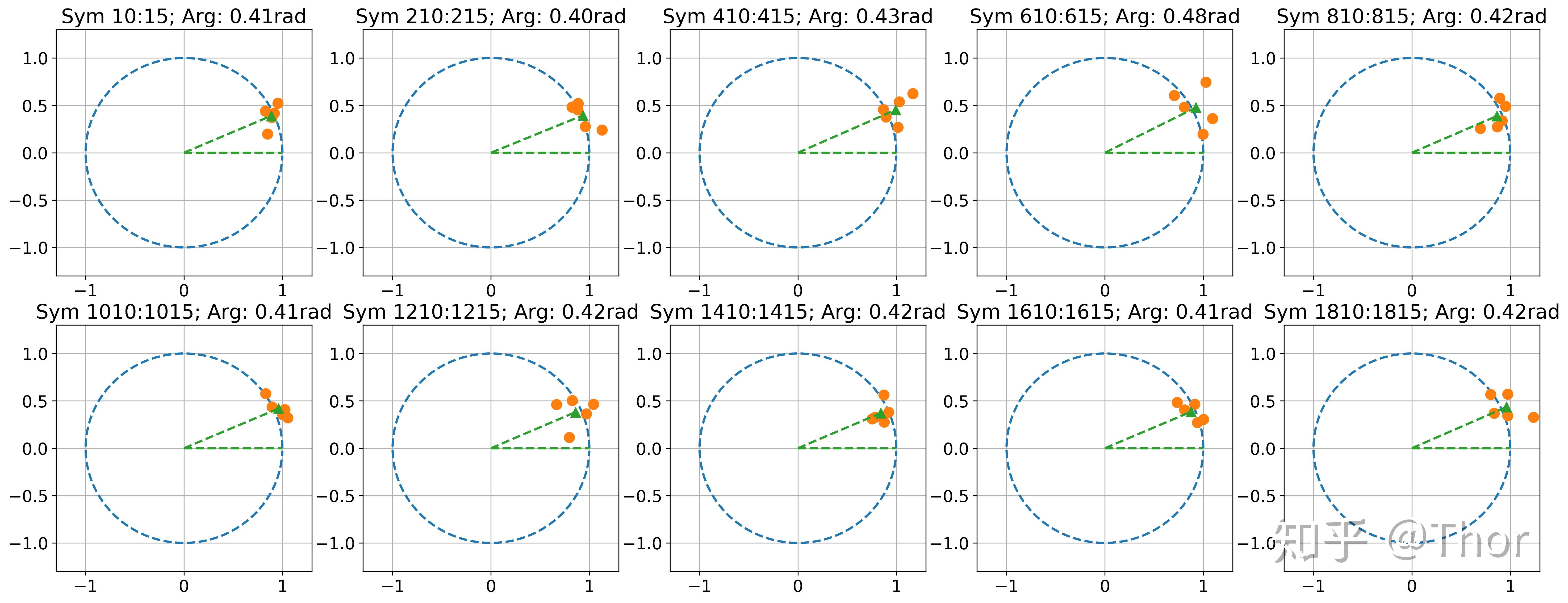
上图我们取N = 5, 做五个点的均匀值可计算得出当下的差频。若是差频不变,在差别的时间段取均匀,计算所得的幅角都应该十分不变。下图我们取十个差别位置的五个symbol做均匀,能够看出其幅角值也是很接近的。仿实中我们设定的差频是1GHz,波特率是60GBd。所以现实的相位差应该是2/15π,约为0.42 rad。能够看到我们在差别位置检测的那个估量值均接近那个现实相位差。
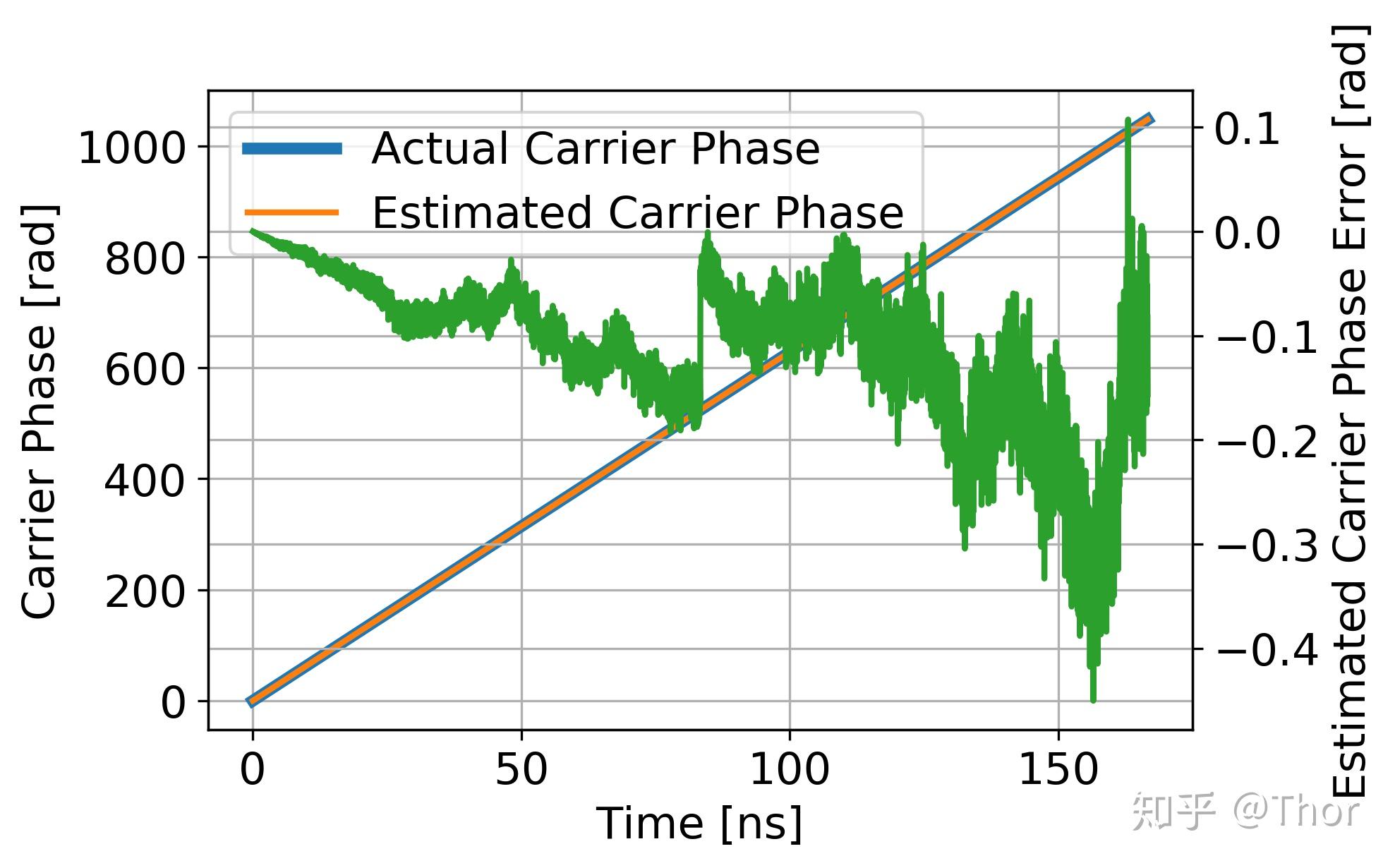
下图所示是10000个symbol的仿实所得的现实的频差相位和用那种算法估量出来的频差相位的比照。
在移除频差之后我们看到已经能看到比力明晰的四个点了。下图所示为每1000个symbol的星座图。
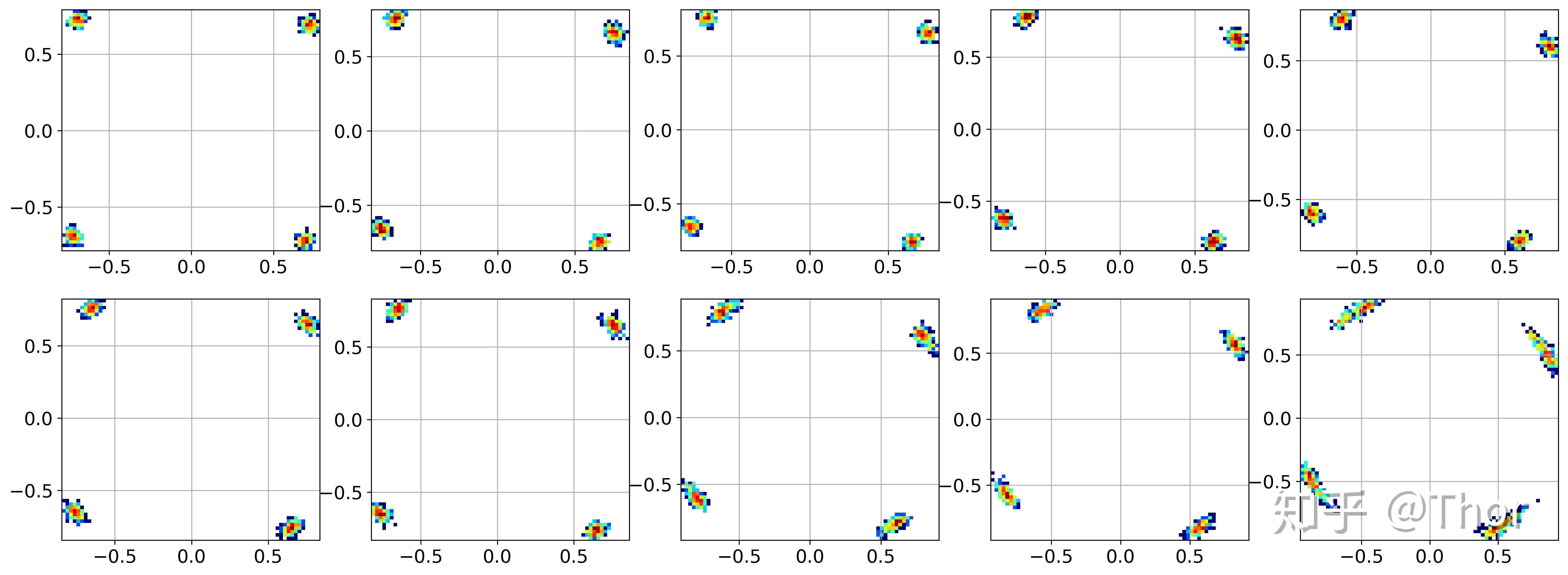
当然还有一些残存的相位没有移除,那些相位误差能够在进一步的相位恢复中移除。当然下一步的相位恢复的信息也能够反应到频差移除那一步,对频差的估量停止优化。那里就不再赘述。
再回到标题问题的问题,频差是几时能够准确地探测出相位呢?我们上文已经讲到若是用四次方的算法探测差频的话,每两个相邻symbol的相位差是 8πΔfT_s ,为制止2π modulus的效应,必需满足以下前提:
在更高阶的QAM中,如16QAM, 64QAM,我们都能够用近似的办法拔取在x,y轴角分线上的星座点停止差频的检测。差别于QPSK所有点的抱负模值都为1,高阶QAM需要判断每个symbol的模值。所以在QPSK 盲平衡恒定模值算法(CMA)的根底上关于高阶QAM又开展出多模值算法(MMA),在高阶QAM的平衡之后能够判断每个点的模值,如16QAM即可拔取最里面的环和最外面的环上的symbol,那些symbol的抱负星座位置都在x和y轴的角分线上。操纵那些点即可用类似的办法检测差频。在抱负情况下,本振激光与信号激光的更大差频前提其实不改动。
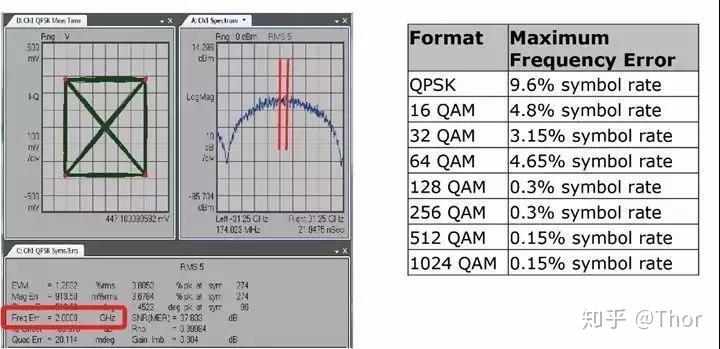
但是高阶QAM关于白噪声和相位噪声愈加敏感,在现实的传输信道中也必然会有非线性的效应。那些都给差频的探测带来必然的挑战。是德(Keysight)的光学调造阐发仪(OMA)给出了其探测差别调造格局的更大允许差频[2]。如下图所示。能够看出在现实情况中,即便是最简单的调造格局QPSK的允许差频,也是小于我们上面得出的结论,12.5% 的symbol rate的。
参考文献:
[1] A. Leven, N. Kaneda, U. Koc and Y. Chen, "Frequency Estimation in Intradyne Reception," in IEEE Photonics Technology Letters, vol. 19, no. 6, pp. 366-368, March15, 2007.doi: 10.1109/LPT.2007.891893
[2] http://www.c-fol.net/m/news/view.php?id=20190425094637
